题目内容
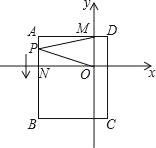
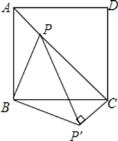
【题目】如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.
【答案】PP′和PC的长分别为4![]() ,6
,6
【解析】
△PAB绕着点B顺时针旋转90°到△P′CB的位置,故∠PBP′=90°,BP′=BP=4,利用勾股定理可求出PP′=4![]() ,由AP=CP′=2,△PCP′为直角三角形即可求出PC.
,由AP=CP′=2,△PCP′为直角三角形即可求出PC.
解:∵△PAB绕着点B顺时针旋转90°到△P′CB的位置,
∴BP′=BP=4,P′C=AP=2,∠PBP′=90°,∠BP′C=∠BPA=135°,
∴△PBP′是等腰直角三角形,
∴PP′=![]() BP=4
BP=4![]() ,∠BP′P=45°,
,∠BP′P=45°,
∴∠PP′C=∠BP′C-∠BP′P=135°-45°=90°,
在Rt△PP′C中,PC=![]() =
=![]() =6.
=6.
答:PP′和PC的长分别为4![]() ,6.
,6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目