题目内容
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.

【答案】(1)y=﹣x2+2x+3;(2)当t=![]() 时,l有最大值,l最大=
时,l有最大值,l最大=![]() ;(3)t=
;(3)t=![]() 时,△PAD的面积的最大值为
时,△PAD的面积的最大值为![]() ;(4)t=
;(4)t=![]() .
.
【解析】试题分析:(1)利用待定系数法即可解决问题;
(2)易知直线AD解析式为y=-x+3,设M点横坐标为m,则P(t,-t2+2t+3),M(t,-t+3),可得l=-t2+2t+3-(-t+3)=-t2+3t=-(t-![]() )2+
)2+![]() ,利用二次函数的性质即可解决问题;
,利用二次函数的性质即可解决问题;
(3)由S△PAD=![]() ×PM×(xD-xA)=
×PM×(xD-xA)=![]() PM,推出PM的值最大时,△PAD的面积最大;
PM,推出PM的值最大时,△PAD的面积最大;
(4)如图设AD的中点为K,设P(t,-t2+2t+3).由△PAD是直角三角形,推出PK=![]() AD,可得(t-
AD,可得(t-![]() )2+(-t2+2t+3-
)2+(-t2+2t+3-![]() )2=
)2=![]() ×18,解方程即可解决问题;
×18,解方程即可解决问题;
试题解析:(1)把点 B(﹣1,0),C(2,3)代入y=ax2+bx+3,
则有![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)在y=﹣x2+2x+3中,令y=0可得0=﹣x2+2x+3,解得x=﹣1或x=3,
∴D(3,0),且A(0,3),
∴直线AD解析式为y=﹣x+3,
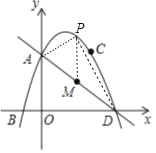
设M点横坐标为m,则P(t,﹣t2+2t+3),M(t,﹣t+3),
∵0<t<3,
∴点M在第一象限内,
∴l=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t=﹣(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,l有最大值,l最大=
时,l有最大值,l最大=![]() ;
;
(3)∵S△PAD=![]() ×PM×(xD﹣xA)=
×PM×(xD﹣xA)=![]() PM,
PM,
∴PM的值最大时,△PAD的面积中点,最大值=![]() ×
×![]() =
=![]() .
.
∴t=![]() 时,△PAD的面积的最大值为
时,△PAD的面积的最大值为![]() .
.
(4)如图设AD的中点为K,设P(t,﹣t2+2t+3).

∵△PAD是直角三角形,
∴PK=![]() AD,
AD,
∴(t﹣![]() )2+(﹣t2+2t+3﹣
)2+(﹣t2+2t+3﹣![]() )2=
)2=![]() ×18,
×18,
整理得t(t﹣3)(t2﹣t﹣1)=0,
解得t=0或3或![]() ,
,
∵点P在第一象限,
∴t=![]() .
.

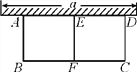
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?
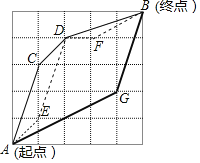
【题目】嘉嘉参加机器人设计活动,需操控机器人在5×5的棋盘格上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R2,其行经位置如图与表所示:
路径 | 编号 | 图例 | 行径位置 |
第一条路径 | R1 | … | A→C→D→B |
第二条路径 | R2 | … | A→E→D→F→B |
第三条路径 | R3 | … | A→G→B |
已知A,B,C,D,E,F,G七点皆落在格线的交点上,且两点之间的路径皆为线段.
(1)分别计算出三条路径的长;
(2)最长的路径是______ (写出编号),最短的路径是 _______(写出编号).