题目内容
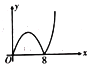
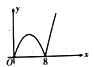
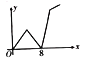
【题目】一次函数y=kx+4与二次函数y=ax2+c的图像的一个交点坐标为（1,2），另一个交点是该二次函数图像的顶点
（1）求k，a，c的值；
（2）过点A（0，m）（0＜m＜4）且垂直于y轴的直线与二次函数y=ax2+c的图像相交于B，C两点，点O为坐标原点，记W=OA2+BC2，求W关于m的函数解析式，并求W的最小值.
【答案】（1）k=-2，a=-2，c=4；（2）
, W取得最小值7.
【解析】
（1）把（1,2）分别代入y=kx+4和y=ax2+c，得k+4=-2和a+c=2，然后求出二次函数图像的顶点坐标为（0,4），可得c=4，然后计算得到a的值；
（2）由A（0，m）（0＜m＜4）可得OA=m，令y=-2x2+4=m，求出B，C坐标，进而表示出BC长度，将OA，BC代入W=OA2+BC2中得到W关于m的函数解析式，求出最小值即可.
解：（1）由题意得，k+4=-2，解得k=-2，
∴一次函数解析式为：y=-2x+4
又二次函数顶点横坐标为0，
∴顶点坐标为（0,4）
∴c=4
把（1,2）带入二次函数表达式得a+c=2，解得a=-2
（2）由（1）得二次函数解析式为y=-2x2+4，令y=m，得2x2+m-4=0
∴
，设B，C两点的坐标分别为（x1，m）（x2，m），则
，
∴W=OA2+BC2=
∴当m=1时，W取得最小值7
【题目】（2018郑州模拟）冬季即将来临，某电器超市销售每台进价分别为300元、255元的A，B两种型号的电热扇，下表是近两周的销售情况：
销售时段 | |||
销售数量 | |||
A种型号 | B种型号 | 销售收入 | |
第一周 | 2台 | 3台 | 1695元 |
第二周 | 5台 | 6台 | 3765元 |
（进价、售价均保持不变，利润
销售收入
进货成本）
（1）分别求出A，B两种型号电热扇的销售单价；
（2）若超市准备用不超过8100元的金额再采购这两种型号的电热扇共30台，求A种型号的电热扇最多能采购多少台？
（3）在（2）的条件下，超市销售完这30台电热扇能否实现利润为2100元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
【题目】复课返校后，为了让同学们进一步了解“新型冠状病毒”的防控知识，某学校组织了一次关于“新型冠状病毒”的防控知识比赛，从问卷中随机抽查了一部分，对调查结果进行了分组统计，并制作了表格与条形统计图（如图）：
分组结果 | 频数 | 频率 |
| 30 | 0.3 |
| 50 |
|
|
| 0.15 |
| 5 |
|
请根据上图完成下面题目：
（1）总人数为 人，
，
．
（2）请求出n的值并补全条形统计图．
（3）若全校有2700人，请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少？
