题目内容
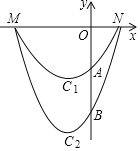
【题目】定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”.如图,抛物线C1与抛物线C2组成一个开口向上的“月牙线”,抛物线C1与抛物线C2与x轴有相同的交点M,N(点M在点N的左侧),与y轴的交点分别为A,B且点A的坐标为(0,﹣3),抛物线C2的解析式为y=mx2+4mx﹣12m,(m>0).
(1)请你根据“月牙线”的定义,设计一个开口向下.“月牙线”,直接写出两条抛物线的解析式;
(2)求M,N两点的坐标;
(3)在第三象限内的抛物线C1上是否存在一点P,使得△PAM的面积最大?若存在,求出△PAM的面积的最大值;若不存在,说明理由.
【答案】(1)抛物线y=﹣x2+2x+3与抛物线y=﹣![]() x2+
x2+![]() x+1所围成的封闭曲线即为开口向下的“月牙线”;(2)M(﹣6,0),N(2,0);(3)存在,点P的坐标为(﹣3,﹣
x+1所围成的封闭曲线即为开口向下的“月牙线”;(2)M(﹣6,0),N(2,0);(3)存在,点P的坐标为(﹣3,﹣![]() )时,△PAM的面积有最大值,最大值为
)时,△PAM的面积有最大值,最大值为![]() .
.
【解析】
(1)根据定义,只要写出的两个抛物线与x轴有着相同的交点,且a的值为负即可;
(2)在解析式y=mx2+4mx-12m中,令y=0解方程即可求出M,N的横坐标,由此可写出M,N两点的坐标;
(3)先根据“月牙线”的定义,设出抛物线C1的一般式,将A点代入即可求得抛物线C1的解析式,再用含t的代数式表示P点坐标,根据S△PAM=S△PMO+S△PAO-S△AOM即可表示△PAM的面积.可根据二次函数的性质求出面积的最大值以及此时P点坐标.
(1)如图1,
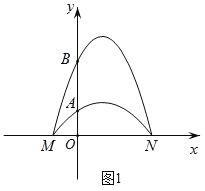
抛物线y=﹣x2+2x+3与抛物线y=﹣![]() x2+
x2+![]() x+1所围成的封闭曲线即为开口向下的“月牙线”(此题答案不唯一);
x+1所围成的封闭曲线即为开口向下的“月牙线”(此题答案不唯一);
(2)在抛物线C2的解析式y=mx2+4mx﹣12m中,
当y=0时,mx2+4mx﹣12m=0,
∵m≠0,
∴x2+4x﹣12=0,
解得,x1=﹣6,x2=2,
∵点M在点N的左边,
∴M(﹣6,0),N(2,0);
(3)存在,理由如下:
如图2,连接AM,PO,PM,PA,
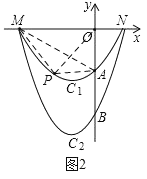
∵抛物线C1和抛物线C2与x轴有着相同的交点,并且开口方向相同,
∴可设抛物线C1的解析式y=nx2+4nx﹣12n(n>0),
∵抛物线C1与y轴的交点为A(0,﹣3),
∴﹣12n=﹣3,
∴n=![]() ,
,
∴抛物线C1的解析式为y=![]() x2+x﹣3,
x2+x﹣3,
∴可设点P的坐标为(t,![]() t2+t﹣3),
t2+t﹣3),
∴S△PAM=S△PMO+S△PAO﹣S△AOM
=![]() ×6×(﹣
×6×(﹣![]() t2﹣t+3)+
t2﹣t+3)+![]() ×3×(﹣t)﹣
×3×(﹣t)﹣![]() ×6×3
×6×3
=﹣![]() t2﹣
t2﹣![]() t,
t,
=﹣![]() (t+3)2+
(t+3)2+![]() ,
,
∵﹣![]() <0,﹣6<t<0,
<0,﹣6<t<0,
∴根据二次函数的图象和性质知,当t=﹣3时,即点P的坐标为(﹣3,﹣![]() )时,△PAM的面积有最大值,最大值为
)时,△PAM的面积有最大值,最大值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 | 分数 | 人数 |
第1组 | 90<x≤100 | 8 |
第2组 | 80<x≤90 | a |
第3组 | 70<x≤80 | 10 |
第4组 | 60<x≤70 | b |
第5组 | 50<x≤60 | 3 |
请根据以上信息,解答下列问题:

(1)求出a,b的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?