题目内容
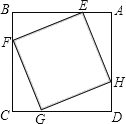
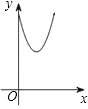
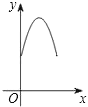
【题目】如图1,菱形ABCD中,∠B=60°,动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B,同时动点Q以每秒2个单位的速度自点B出发沿折线B﹣C﹣D运动到点D.图2是点P、Q运动时,△BPQ的面积S随时间t变化关系图象,则a的值是( )
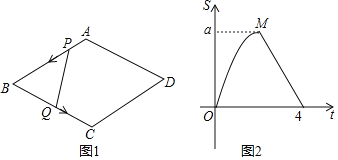
A.2B.2.5C.3D.2![]()
【答案】D
【解析】
根据图1和图2中的数据即可作出判断.
由图2得,t=4时两点停止运动,
∴点P以每秒1个单位速度从点A运动到点B用了4秒,
∴AB=4,
∵点Q运动到点C之前和之后,△BPQ面积算法不同,即t=2时,S的解析式发生变化
∴图2中点M对应的横坐标为2,此时P为AB中点,点C与点Q重合,
连接AC,
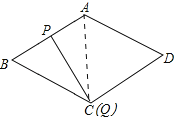
∵菱形ABCD中,AB=BC=4,∠B=60°,
∴△ABC是等边三角形,
∴CP⊥AB,BP=![]() AB=2,
AB=2,
∴CP=![]() ,
,
∴a=S=![]() BPCP=
BPCP=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
故选D.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
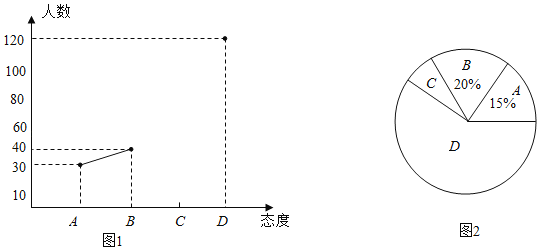
【题目】为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 | 分数 | 人数 |
第1组 | 90<x≤100 | 8 |
第2组 | 80<x≤90 | a |
第3组 | 70<x≤80 | 10 |
第4组 | 60<x≤70 | b |
第5组 | 50<x≤60 | 3 |
请根据以上信息,解答下列问题:

(1)求出a,b的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?