题目内容
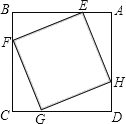
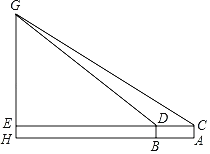
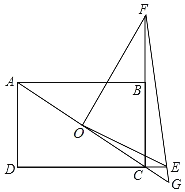
【题目】如图,在矩形ABCD中,AB=9,AD=6,点O为对角线AC的中点,点E在DC的延长线上且CE=1.5,连接OE,过点O作OF⊥OE交CB延长线于点F,连接FE并延长交AC的延长线于点G,则![]() =_____.
=_____.
【答案】![]()
【解析】
作OM⊥CD于M,ON⊥BC于N,根据三角形中位线定理分别求出OM、ON,根据勾股定理求出OE,根据相似三角形的性质求出FN,得到FC的长,证明△GFC∽△GOE,根据相似三角形的性质列出比例式,代入计算得到答案.
解:作OM⊥CD于M,ON⊥BC于N,
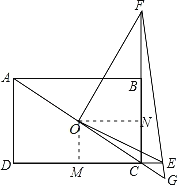
∵四边形ABCD为矩形,
∴∠D=90°,∠ABC=90°,
∴OM∥AD,ON∥AB,
∵点O为AC的中点,
∴OM=![]() AD=3,ON=
AD=3,ON=![]() AB=4.5,CM=4.5,CN=3,
AB=4.5,CM=4.5,CN=3,
∵CE=1.5,
∴ME=CM+CE=6,
在Rt△OME中,OE=![]() =3
=3![]() ,
,
∵∠MON=90°,∠EOF=90°,
∴∠MOE+∠NOE=∠NOF+∠NOE=90°,
∴∠MOE=∠NOF,又∠OME=∠ONF=90°,
∴△OME∽△ONF,
∴![]() ,即
,即![]() ,
,
解得,FN=9,
∴FC=FN+NC=12,
∵∠FOE=∠FCE=90°,
∴F、O、C、E四点共圆,
∴∠GFC=∠GOE,又∠G=∠G,
∴△GFC∽△GOE,
∴![]() ,
,
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】小颖“综合与实践”小组学习了三角函数后,开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,如表是不完整测量数据.
课题 | 测量旗杆的高度 | |||
成员 | 组长:小颖,组员:小明,小刚,小英 | |||
测量工具 | 测量角度的仪器,皮尺等 | |||
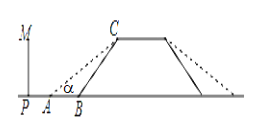
测量示意图 |
| 说明: 线段GH表示学校旗杆,测量角度的仪器的高度AC=BD=1.62m,测点A,B与H在同一水平直线上,A,B之间的距离可以直接测得,且点G,H,A,B,C,D都在同一竖直平面内,点C,D,E在同一条直线上,点E在GH上. | ||
测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
∠GCE的度数 | 30.6° | 31.4° | 31° | |
∠GDE的度数 | 36.8° | 37.2° | 37° | |
A,B之间的距离 | 10.1m | 10.5m | m | |
… | … | |||
(1)任务一:完成表格中两次测点A,B之间的距离的平均值.
(2)任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆GH的高度.(精确到0.1m)(参考数据:sin31°≈0.51,cos31°≈0.86,tan31°≈0.60,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)