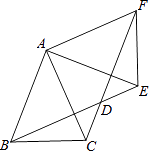
题目内容
【题目】如图,已知CA=CB,点E,F在射线CD上,满足∠BEC=∠CFA,且∠BEC+∠ECB+∠ACF=180°.
(1)求证:△BCE≌△CAF;
(2)试判断线段EF,BE,AF的数量关系,并说明理由.
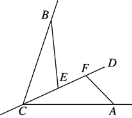
【答案】(1)见解析;(2) AF+EF=BE,理由见解析.
【解析】
(1)根据题意,结合图形依据AAS可以证明△BCE≌△CAF;
(2)根据(1)的结论可得AF=CE,CF=BE即可证出结论.
(1)证明:∵∠BEC=∠CFA,
∠BEC+∠ECB+∠ACF=180°,
∠CFA+∠ACF+∠FAC=180°,
∴∠BCE=∠FAC,
在△BCE和△CAF中,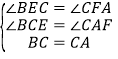 ,
,
∴△BCE≌△CAF(AAS);
(2)解:AF+EF=BE,理由如下:
∵△BCE≌△CAF,∴AF=CE,CF=BE,
∵CE+EF=CF,∴AF+EF=BE.

练习册系列答案
相关题目