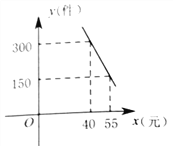
��Ŀ����
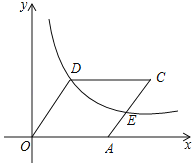
����Ŀ����ͼ��ֱ��y=-![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C����֪���κ�����ͼ����B��C�͵�A(-1��0)��
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C����֪���κ�����ͼ����B��C�͵�A(-1��0)��
(1)��B��C��������꣮
(2)��ö��κ����Ľ���ʽ��
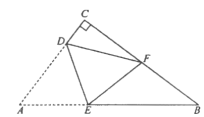
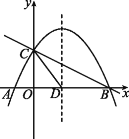
(3)�������ߵĶԳ�����x��Ľ���Ϊ��D�����������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ���������?������ڣ�ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
(4)��E���߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���ı���CDBF��������?����ı���CDBF������������ʱ��E�����꣮
���𰸡���1��B(4��0)��C(0��2)����2��y=-![]() x2+
x2+![]() x+2����3�����ڣ�P1(
x+2����3�����ڣ�P1(![]() ��4)��P2(
��4)��P2(![]() )��P3(
)��P3(![]() ��-
��-![]() )����4����a=2ʱ��S�ı���CDBF�����ֵ=
)����4����a=2ʱ��S�ı���CDBF�����ֵ=![]() ����ʱE(2��1)��
����ʱE(2��1)��
��������
��1���ֱ������ʽy=-![]() x+2��x=0��y=0�������B����C�����ꣻ
x+2��x=0��y=0�������B����C�����ꣻ
��2�����κ����Ľ���ʽΪ![]() ������A��B��C������������ʽ�����a��b��c��ֵ������������κ����Ľ���ʽ��
������A��B��C������������ʽ�����a��b��c��ֵ������������κ����Ľ���ʽ��
��3���ɣ�2���Ľ���ʽ����������꣬���ɹ��ɶ������CD��ֵ�����Ե�CΪԲ�ģ�CDΪ�뾶�������Գ�����![]() ���Ե�DΪԲ�ģ�CDΪ�뾶��Բ���Գ�����
���Ե�DΪԲ�ģ�CDΪ�뾶��Բ���Գ�����![]() ��
��![]() ����CE��ֱ�Գ����ڵ�E���ɵ��������ε����ʺ��ɶ����Ϳ���������ۣ�
����CE��ֱ�Գ����ڵ�E���ɵ��������ε����ʺ��ɶ����Ϳ���������ۣ�
��4�����E������Ϊ![]() ���Ϳ��Ա�ʾ��F�����꣬��
���Ϳ��Ա�ʾ��F�����꣬��![]() ���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
�⣺(1)��y=-![]() x+2�У���x=0���ɵ�y=2����y=0���ɵ�x=4��
x+2�У���x=0���ɵ�y=2����y=0���ɵ�x=4��
��B(4��0)��C(0��2)��
(2)����κ����Ľ���ʽΪy=ax2+bx+c��
����A��B��C������������ʽ����
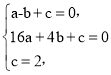 ��
��
���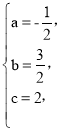
���ö��κ����Ľ���ʽΪy=-![]() x2+
x2+![]() x+2��
x+2��
(3)���ڣ���y=-![]() x2+
x2+![]() x+2��
x+2��
��y=-![]() (x-
(x-![]() )2+
)2+![]() ��
��
�������ߵĶԳ�����ֱ��x=![]() ����OD=
����OD=![]() ��
��
��C(0��2)����OC=2��
��Rt��OCD�У��ɹ��ɶ�������CD=![]() ��
��
�ߡ�PCD����CDΪ���ĵ��������Σ�
��CP1=DP2=DP3=CD��
��ͼ����ʾ����CH�ͶԳ����ڵ�H����HP1=HD=2��
��DP1=4��
��P1(![]() ��4)��P2(
��4)��P2(![]() )��P3(
)��P3(![]() ��-
��-![]() )��
)��
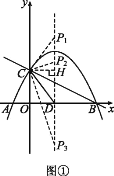
(4)��B(4��0)��C(0��2)��
��ֱ��BC�Ľ���ʽΪy=-![]() x+2��
x+2��
��ͼ�ڣ�����C��CM��EF�ڵ�M��
��E(a��-![]() a+2)��F(a��-
a+2)��F(a��-![]() a2+
a2+![]() a+2)��
a+2)��
��EF=-![]() a2+
a2+![]() a+2-(-
a+2-(-![]() a+2)=-
a+2)=-![]() a2+2a(0��a��4)��
a2+2a(0��a��4)��
��S�ı���CDBF=S��BCD+S��CEF+S��BEF=![]() BD��OC+
BD��OC+![]() EF��CM+
EF��CM+![]() EF��BN
EF��BN
=![]() ��(4-
��(4-![]() )��2+
)��2+![]() a(-
a(-![]() a2+2a)+
a2+2a)+![]() (4-a)( -
(4-a)( -![]() a2+2a)
a2+2a)
=-a2+4a+![]()
=-(a-2)2+![]() ��
��
�൱a=2ʱ��S�ı���CDBF�����ֵ=![]() ����ʱE(2��1)��
����ʱE(2��1)��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ���������������̳��ﹺ���ܺ���90Ԫ����Ʒ�ס��ҡ��������Σ����мĵ�����20Ԫ���ҵĵ�����40Ԫ������Ʒ��һ�ι���������ǵڶ��ι�������������������Ʒ��һ�ι�������������Ʒ�ڶ��ι����������ȣ����ι�����Ʒ�ס��ҡ������������ܷ������±���
������Ʒ�� ����(��) | ������Ʒ�ҵ� ����(��) | ������Ʒ���� ����(��) | �����ܷ���(Ԫ) | |
��һ�ι��� | 4 | 440 | ||
�ڶ��ι��� | 7 | 490 |
(1)�����ι���ס��ҡ���������Ʒ���������ֱ��Ƕ��٣�
(2)���������̳�������������������������ǰ��������Ʒ�ס��ҡ�������������Ʒ�������ܺ�Ϊa�������й�������Ʒ�����Ǽ���Ʒ������3���������ܷ���Ϊ1 280Ԫ����a����Сֵ��