题目内容
【题目】已知:等腰![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、点
、点![]() .
.
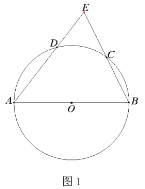
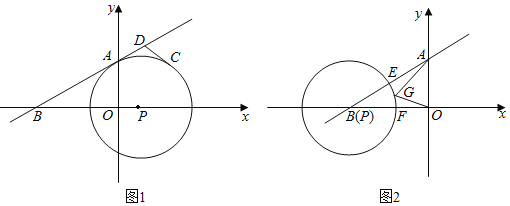
(1)如图1,求证:点![]() 为弧
为弧![]() 的中点;
的中点;
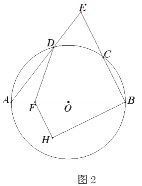
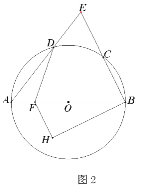
(2)如图2,点![]() 为直径
为直径![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交过点
,交过点![]() 且垂直于
且垂直于![]() 的直线于点
的直线于点![]() ,连接
,连接![]() ,
,![]() ,设
,设![]()
![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
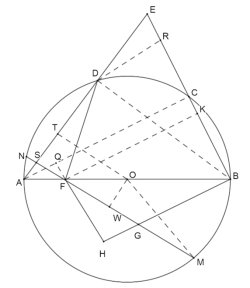
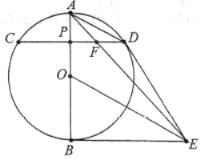
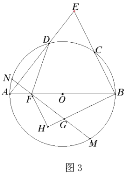
(3)如图3,在(2)的条件下,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]()
![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)见详解;(2)m=n+45;(3)![]()
【解析】
(1)连接AC,根据题意知,∠ACB=90°,由AB=AE,等腰三角形三线合一可得AC平分∠BAE,相等的圆周角所对的弧相等即可证得;
(2)根据FH∥BC,推出∠ABE=∠BFH=∠CED=m°,由外角性质知DFB=∠A+∠ADF,利用三角形内角和180°以及∠DFH=135°,代换可得m与n的函数关系式;
(3)设∠DAC=∠BAC=![]() ,由(2)的结论可推出MN⊥AD,通过△BER≌△FGH,FG=DE,再利用勾股定理计算WM,可得出MN=2WM即可得结果.
,由(2)的结论可推出MN⊥AD,通过△BER≌△FGH,FG=DE,再利用勾股定理计算WM,可得出MN=2WM即可得结果.
(1)连接AC,
∵ AB是直径,
∴∠ACB=90°,
∵AB=AE,
∴AC平分∠BAE,
∴∠BAC=∠EAC,
∴点C是弧BD的中点;
(2)∵AB=AE,FH∥BC,
∴∠BFH=∠EBA=∠E=m°,∠A=180°-2m°,
∵∠ADF=n°,
∴∠BFD=∠A+∠ADF=180°-2m°+n°,
又∵∠DFH=135°,∠DFH=∠BFH+∠BFD,
∴135°=m°+180°-2m°+n°,
∴m=45+n,
∴m与n的函数关系式为:m=45+n,
故答案为:m=45+n;
(3)设∠DAC=∠BAC=![]() ,
,
由(2)∠CED=∠ADF+45°,
∴∠ADF=90°-![]() -45°=45°-
-45°=45°-![]() ,
,
∴∠DFB=45°-![]() +2
+2![]() =45°+
=45°+![]() ,
,
∵∠BFM+2∠BFD=180°,
∴∠BFM=90°-2![]() ,
,
∵∠BFH=∠AFQ=90°-![]() ,
,
∴∠HFG=90°-![]() -(90°-2
-(90°-2![]() )=
)=![]() ,
,
∴∠BFG+∠E=180°,
∴∠ESM=90°,即MN⊥AD,
导角:∠FDB=∠DFB=45°+![]() ,
,
∴BF=BD,
又∵∠E=∠BFH=90°-![]() ,
,
∴∠DBR=∠FBH=![]() ,
,
∴△BDR≌△BHF,
∴FH=DR,
可推出△BER≌△FGH,
∴FG=DE,
∵FG:AB=2:5,
∴DE:AE=2:5,
设DE=2![]() ,AE=5
,AE=5![]() =AB,
=AB,
∴AD=3![]() ,BD=4
,BD=4![]() ,
,
∴tan2![]() =
=![]() ,tan
,tan![]() =
=![]() ,
,
∴tan∠ADF=tan(45°-![]() )=
)=![]() ,
,
∵CB-FH=CK=QF=4,
∴AF=4![]() ,
,
∴SF=![]() ×4=
×4=![]() ,
,
AS=![]() ×3=
×3=![]() ,
,
DS=![]() ×3=
×3=![]() ,
,
AD=AS+DS=12![]() ,
,
∴TD-![]() AD=6
AD=6![]() ,
,
∴ST=OW=DS-DT=![]() ,
,
∴AB=![]() ×5=20
×5=20![]() ,
,
∴r=10![]() ,
,
∴WM=![]() =
=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.