题目内容
【题目】如图，在平面直角坐标系中，一次函数y＝
x+2的图象与y轴交于A点，与x轴交于B点，⊙P的半径为
，其圆心P在x轴上运动．
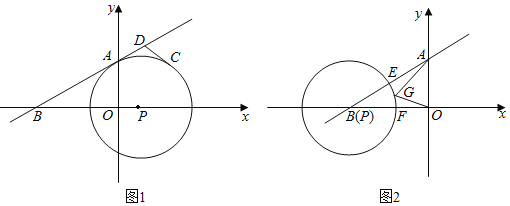
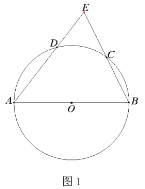
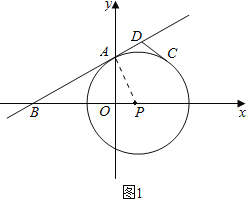
（1）如图1，当圆心P的坐标为（1，0）时，求证：⊙P与直线AB相切；
（2）在（1）的条件下，点C为⊙P上在第一象限内的一点，过点C作⊙P的切线交直线AB于点D，且∠ADC＝120°，求D点的坐标；
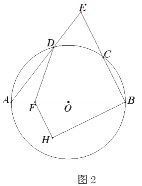
（3）如图2，若⊙P向左运动，圆心P与点B重合，且⊙P与线段AB交于E点，与线段BO相交于F点，G点为弧EF上一点，直接写出AG+OG的最小值 ．
【答案】（1）见解析；（2）D（
，
+2）；（3）
．
【解析】
（1）连接PA，先求出点A和点B的坐标，从而求出OA、OB、OP和AP的长，即可确定点A在圆上，根据相似三角形的判定定理证出△AOB∽△POA，根据相似三角形的性质和等量代换证出PA⊥AB，即可证出结论；
（2）连接PA，PD，根据切线长定理可求出∠ADP＝∠PDC＝
∠ADC＝60°，利用锐角三角函数求出AD，设D（m，m+2），根据平面直角坐标系中任意两点之间的距离公式求出m的值即可；
（3）在BA上取一点J，使得BJ＝
，连接BG，OJ，JG，根据相似三角形的判定定理证出△BJG∽△BGA，列出比例式可得GJ＝AG，从而得出AG+OG＝GJ+OG，设J点的坐标为（n，n+2），根据平面直角坐标系中任意两点之间的距离公式求出n，从而求出OJ的长，然后根据两点之间线段最短可得GJ+OG≥OJ，即可求出结论．
（1）证明：如图1中，连接PA．
∵一次函数y＝x+2的图象与y轴交于A点，与x轴交于B点，
∴A（0，2），B（﹣4，0），
∴OA＝2，OB＝4，
∵P（1，0），
∴OP＝1，
∴OA2＝OBOP，AP=
∴
＝
，点A在圆上
∵∠AOB＝∠AOP＝90°，
∴△AOB∽△POA，
∴∠OAP＝∠ABO，
∵∠OAP+∠APO＝90°，
∴∠ABO+∠APO＝90°，
∴∠BAP＝90°，
∴PA⊥AB，
∴AB是⊙P的切线．
（2）如图1﹣1中，连接PA，PD．
∵DA，DC是⊙P的切线，∠ADC＝120°，
∴∠ADP＝∠PDC＝∠ADC＝60°，
∴∠APD＝30°，
∵∠PAD＝90°
∴AD＝PAtan30°＝
，
设D（m，m+2），
∵A（0，2），
∴m2+（m+2﹣2）2＝
，
解得m＝±，
∵点D在第一象限，
∴m＝，
∴D（，+2）．
（3）在BA上取一点J，使得BJ＝，连接BG，OJ，JG．
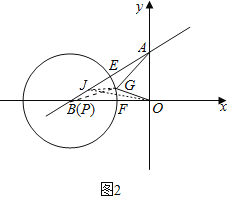
∵OA＝2，OB＝4，∠AOB＝90°，
∴AB＝
＝
＝2
，
∵BG＝，BJ＝，
∴BG2＝BJBA，
∴
＝
，
∵∠JBG＝∠ABG，
∴△BJG∽△BGA，
∴
＝
＝，
∴GJ＝AG，
∴AG+OG＝GJ+OG，
∵BJ＝，设J点的坐标为（n，n+2），点B的坐标为（-4,0）
∴（n+4）2+（n+2）2＝
，
解得：n=-3或-5（点J在点B右侧，故舍去）
∴J（﹣3，），
∴OJ＝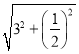
＝
∵GJ+OG≥OJ，
∴AG+OG≥，
∴AG+OG的最小值为．
故答案为．
