题目内容
【题目】如图,![]() 中,
中,![]() 为
为![]() 上的中线,
上的中线,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,则
,则![]() _____.
_____.

【答案】7
【解析】
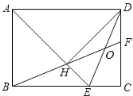
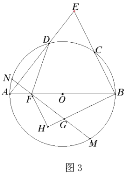
延长AD到G,使DG=AD,连接BG,CG,GF,过点C作CH⊥BG于H,过作CN⊥BE于N,由平行四边形的判定可证四边形ABGC是平行四边形,可得AC∥BG,AC=BG,AB=CG,由“AAS”可证△BCN≌△△BCH,可得BN=BH,CN=CH,由三个角是直角是四边形是矩形可证四边形CFGH是矩形,可得HG=CF=1,由线段的数量关系可求EN的长,由直角三角形的性质可求CN=CH=4![]() ,由勾股定理可求CG的长,即可求解.
,由勾股定理可求CG的长,即可求解.
如图,延长AD到G,使DG=AD,连接BG,CG,GF,过点C作CH⊥BG于H,过作CN⊥BE于N,
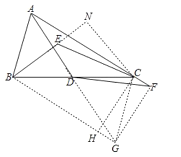
∵AD为BC上的中线,
∴BD=CD,且DG=AD,
∴四边形ABGC是平行四边形,
∴AC∥BG,AC=BG,AB=CG,
∴∠ACB=∠CBG,且∠EBC=∠ACB,
∴∠EBC=∠CBG,且∠N=∠CHB=90°,BC=BC,
∴△BCN≌△BCH(AAS),
∴BN=BH,CN=CH,
∵ACBE=5,
∴BGBE=BH+HGBE=BN+HGBE=EN+HG=5,
∵AD=DF,AD=DG,
∴AD=DF=DG,
∴∠AFG=90°,
∵AC∥BG,CH⊥BG,
∴CH⊥AF,且CH⊥BG,∠AFG=90°,
∴四边形CFGH是矩形,
∴CF=HG=1,
∴EN=4,
∵∠BEC=120°,
∴∠NEC=60°,且∠N=90°,
∴NC=ENtan60°=![]() EN=4
EN=4![]() ,
,
∴CH=4![]() ,
,
∴AB=CG=![]() =7,
=7,
故答案为:7.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目