题目内容
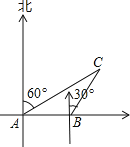
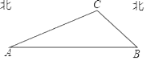
【题目】如图所示,要在某东西走向的A、B两地之间修一条笔直的公路,在公路起点A处测得某农户C在A的北偏东68°方向上.在公路终点B处测得该农户c在点B的北偏西45°方向上.已知A、B两地相距2400米.
(1)求农户c到公路B的距离;(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
(2)现在由于任务紧急,要使该修路工程比原计划提前4天完成,需将该工程原定的工作效率提高20%,求原计划该工程队毎天修路多少米?
【答案】(1)农户C到公路的距离![]() 米;(2)原计划该工程队毎天修路100米.
米;(2)原计划该工程队毎天修路100米.
【解析】
(1)农户C到公路的距离,也就是求C到AB的距离.要构造直角三角形,再解直角三角形;
(2)设原计划y天完成,则由等量关系“原工作效率×(1+25%)=提前完成时的工作效率”列方程求解.
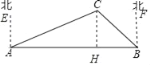
(1)如图,过C作CH⊥AB于H.
设CH=x,
由已知有∠EAC=68°,∠FBC=45°,
则∠CAH=22°,∠CBA=45°.
在Rt△BCH中,BH=CH=x,
在Rt△HAC中,tan∠HAC=![]() ,
,
∴HA=![]() ,
,
∵AH+HB=AB,
∴x+![]() x=2400,
x=2400,
解得x=![]() ,
,
∴农户C到公路的距离![]() 米.
米.
(2)设原计划完成这项工程需要y天,则实际完成工程需要(y﹣4)天.
根据题意得:![]() =(1+20%)×
=(1+20%)×![]() ,
,
解得:y=24.
经检验知:y=24是原方程的根,
2400÷24=100(米).
答:原计划该工程队毎天修路100米.

练习册系列答案
相关题目