题目内容
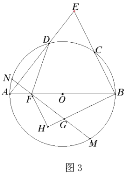
【题目】如图,![]() 为
为![]() 直径,
直径,![]() 点为半径
点为半径![]() 上异于
上异于![]() 点和
点和![]() 点的一个点,过
点的一个点,过![]() 点作与直径
点作与直径![]() 垂直的弦
垂直的弦![]() ,连接
,连接![]() ,作
,作![]() ,
,![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() 、
、![]() ,
,![]() 交
交![]() 于
于![]() 点.
点.
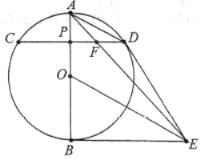
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() ;
;
(3)请猜想![]() 与
与![]() 的数量关系,并加以证明.
的数量关系,并加以证明.
【答案】(1)证明见解析;(2)2;(3)![]() ,理由见解析
,理由见解析
【解析】
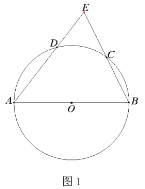
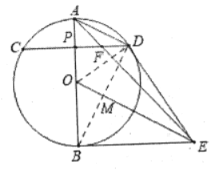
(1)如图1,连接OD,利用平行线与等腰三角形的性质证明![]() ,证明△BOE≌△DOE,则∠ODE=∠OBE=90°,可得结论;
,证明△BOE≌△DOE,则∠ODE=∠OBE=90°,可得结论;
(2)连接BD,因为OP垂直于CD,由垂径定理可证得弧AC等于弧AD,∠ABD等于∠ADP,由直角三角形ADB中sin∠ABD=sin∠ADP=![]() ,可得,AD=
,可得,AD= ![]() AB,可得AD的长;
AB,可得AD的长;
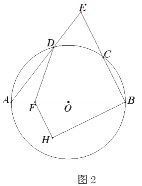
(3)先证明△APF∽△ABE,得![]() ,由△ADP∽△OEB,得
,由△ADP∽△OEB,得![]() ,可得PD=2PF,可得结论.
,可得PD=2PF,可得结论.
证明:(1)如图,连接![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为
为![]() 的切线
的切线
(2)连接![]() ,
,
![]() 是
是![]() 的直径,
的直径,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
(3)答:结论:![]()
证明:![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目