Question

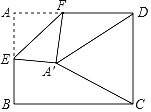
【题目】如图，在矩形纸片ABCD中，AB＝4，BC＝4，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A'EF，连接A'C，A'D，则当△A'DC是以A'D为腰的等腰三角形时，FD的长是_____．

Answer 1

【答案】4﹣2或3

【解析】

存在两种情况：当A′D=DC，连接ED，勾股定理求得ED的长，可判断E，A′，D三点共线，根据勾股定理即可得到结论；当A′D=A′C，证明AEA′F是正方形，于是得到结论．

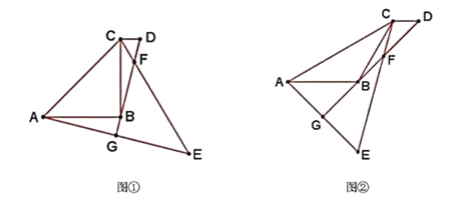
解：①当A′D=DC时，如图1，连接ED，

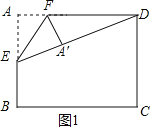
∵点E是AB的中点，AB=4，BC=4，四边形ABCD是矩形，
∴AD=BC=4，∠A=90°，
∴DE==6，
∵将△AEF沿EF所在直线翻折，得到△A'EF，
∴A′E=AE=2，
∵A′D=DC=AB=4，
∴DE=A′E+A′D=6，
∴点E，A′，D三点共线，
∵∠A=90°，
∴∠FA′E=∠FA′D=90°，

设AF=x，则A′F=x，FD=4-x，
在Rt△FA′D中，42+x2=（4-x）2，
解得：x=，
∴FD=3；
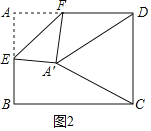
②当A′D=A′C时，如图2，
∵A′D=A′C，
∴点A′在线段CD的垂直平分线上，
∴点A′在线段AB的垂直平分线上，
∵点E是AB的中点，
∴EA′是AB的垂直平分线，
∴∠AEA′=90°，
∵将△AEF沿EF所在直线翻折，得到△A'EF，
∴∠A=∠EA′F=90°，AF=FA′，
∴四边形AEA′F是正方形，
∴AF=AE=2，
∴DF=4-2，
故答案为：4-2或3．