题目内容
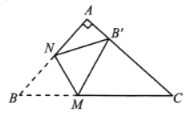
【题目】如图，某渔船在海面上朝正东方向匀速航行，在A处观测到灯塔M在北偏东60°方向上，且AM =
海里，那么该船继续航行______海里可使渔船到达离灯塔距离最近的位置.
【答案】
．
【解析】
根据题意知，过M作东西方向的垂线,设垂足为N，MN即为渔船离灯塔距离最近的距离，在Rt△AMN中，可知∠MAN= 30，AM = 
海里，利用余弦定理即可求出轮船航行的最短距离AN．
如图，过M作东西方向的垂线,设垂足为N，
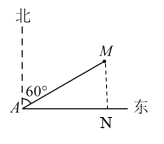
易知:∠MAN = 90°- 60° = 30°，
在Rt△AMN中，
∵∠ANM = 90°，∠MAN= 30，AM = 海里，
∴AN=AM×cos∠MAN= ×
海里，
故该船继续航行海里可使渔船到达离灯塔距离最近的位置．
故答案为．
练习册系列答案
相关题目
【题目】为了解学生每天的睡眠情况，某初中学校从全校800名学生中随机抽取了40名学生，调查了他们平均每天的睡眠时间（单位：h），统计结果如下：9，8，10.5，7，9，8，10，9.5，8，9，9.5，7.5，9.5，9，8.5，7.5，10，9.5，8，9，7，9.5，8.5，9，7，9，9，7.5，8.5，8.5，9，8，7.5，9.5，10，9.5，8.5，9，8，9．在对这些数据整理后，绘制了如图的统计图表：
睡眠时间分组统计表：
组别 | 睡眠时间分组 | 人数（频数） |
1 | 7≤t＜8 | m |
2 | 8≤t＜9 | 11 |
3 | 9≤t＜10 | n |
4 | 10≤t＜11 | 4 |
请根据以上信息，解答下列问题：
（1）m＝ ，n＝ ，a＝ ，b＝ ；
（2）抽取的这40名学生平均每天睡眠时间的中位数落在 组（填组别）；在扇形统计图中，第4组所在扇形的圆心角是 度；
（3）如果按照学校要求，学生平均每天的睡眠时间应不少于9h．请估计该校学生中睡眠时间符合要求的人数．
