题目内容
【题目】在矩形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,连接
上,连接![]() 将
将![]() 沿
沿![]() 折叠,若点
折叠,若点![]() 的对称点
的对称点![]() 到
到![]() 的距离为
的距离为![]() ,则
,则![]() 的长为______________________.
的长为______________________.
【答案】![]() 或
或![]()
【解析】
分两种情况进行分类讨论:(1)当![]() 在矩形内部到AD的距离为1;(2)点
在矩形内部到AD的距离为1;(2)点![]() 在矩形外部到AD的距离为1.
在矩形外部到AD的距离为1.
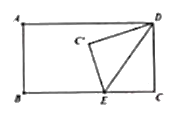
解:设CE=x.
当C在矩形内部时,如图,过点C作FG垂直AD,交AD于点F,BC于点G.
由折叠的性质,得D![]() =DC=2,∠
=DC=2,∠![]() =90°,CE=
=90°,CE=![]() E.
E.
在Rt△D![]() F中,F
F中,F![]() =1,由勾股定理,得DF=
=1,由勾股定理,得DF=![]() =
=![]() .
.
又∵∠G![]() E=∠FD
E=∠FD![]() ,∠
,∠![]() GE=∠
GE=∠![]() FD=90°,
FD=90°,
∴△G![]() E
E![]() △FD
△FD![]() ,∴
,∴![]() =
=![]() .
.
∴x=![]() .
.
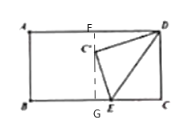
当C在矩形内部时,如图,过点C’作BC的平行线,交CD的延长线G,过点E作EQ⊥QG于点Q,则EQ=2+1=3,DG=1.
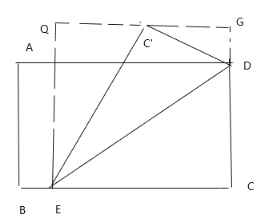
由折叠的性质,得EC’=CE,C’D=CD=2.
在Rt△D![]() G中,DG =1,由勾股定理,得C’G=
G中,DG =1,由勾股定理,得C’G=![]() =
=![]() .
.
∵∠QEC’=∠GC’D,∠Q=∠G,
∴△Q![]() E
E![]() △GD
△GD![]() ,
,![]() =
=![]() .
.
∴x=2![]() .
.
∴CE的长为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】为了迎接疫情彻底结束后的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表
运动鞋价格 | 甲 | 乙 |
进价(元/双) |
|
|
售价(元/双) |
|
|
已知:用![]() 元购进甲种运动鞋的数量与用
元购进甲种运动鞋的数量与用![]() 元购进乙种运动鞋的数量相同.
元购进乙种运动鞋的数量相同.
![]() 求
求![]() 的值;
的值;
![]() 要使购进的甲、乙两种运动鞋共
要使购进的甲、乙两种运动鞋共![]() 双的总利润(利润
双的总利润(利润![]() 售价
售价![]() 进价)不少于
进价)不少于![]() 元,且甲种运动鞋的数量不超过
元,且甲种运动鞋的数量不超过![]() 双,问该专卖店共有几种进货方案;
双,问该专卖店共有几种进货方案;
![]() 在
在![]() 的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠
的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠![]() 元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?