Question

【题目】已知：点和是一次函数与反比例函数图象的连个不同交点，点关于轴的对称点为,直线以及分别与轴交于点和.

（1）求反比例函数的表达式；

（2）若，求的取值范围.

Answer 1

【答案】（1）；（2） 或.

【解析】

（1）将点A（-1，-4）代入反比例函数解析式，即可得m的值；

（2）分两种情况讨论：当P在第一象限或第三象限时，过点作于点，交x轴于点， ，通过相似的性质求出AC的长，然后求出点P的坐标，求出一次函数的解析式，即可求出k的取值范围.

解：（1）将点A（-1，-4）代入反比例函数解析式，即可得m=4，

∴反比例函数解析式是；

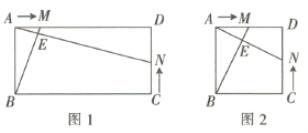
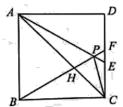
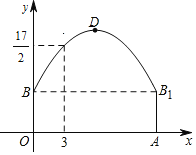
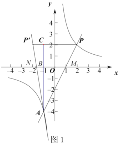
（2）分两种情况讨论：当P在第一象限时，如图1，当时，过点作于点，交x轴于点，

∵，

∴，，

∴，

∴AC=6,

∴点P的纵坐标是2，

把y=2代入中得x=2，

∴点P的坐标是（2，2），

∴，

∴，

∴一次函数的解析式为y=2x-2,

当时，AC>6,此时点P的纵坐标大于2，k的值变大，所以k>2，

∴；

当P在第三象限时，如图2，当时，过点作于点，交x轴于点，

∵，

∴，，

∴，

∴AC=6,

∴点P的纵坐标是-10，

把y=-10代入中得x= ，

∴点P的坐标是（，-10），

∴，

∴，

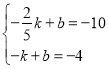∴一次函数的解析式为y=-10x-14,

当时，AC>6,此时点P的纵坐标小于-10，k的值变小，所以k<-10，

∴；

综上所述，的取值范围或.