��Ŀ����
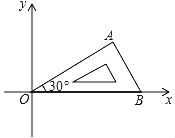
����Ŀ���涨����һ���غϣ��ҽǵ����ߵ�����һ������������ı��ν�����Ƕ���ı���������ͼ���ı���ABCD��AMPN����Ƕ���ı��Σ�
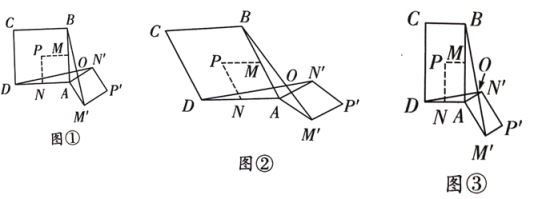
��1����������
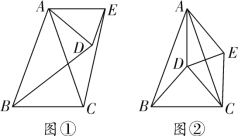
��ͼ�٣�Ƕ���ı���ABCD��AMPN���������Σ��ְ�������AMPN��AΪ����˳ʱ����ת150���õ�������AM'P'N'������BM'��DN'���ڵ�O����BM'��DN'��������ϵΪ_____��λ�ù�ϵΪ_____��
��2�����̽��
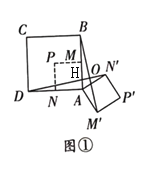
��ͼ�ڣ�����1���е������λ������Σ���BAD=��MAN=60�������������䣬��1���еĽ��ۻ�������? ����������˵�����ɣ������������������ȷ�Ľ��ۣ���˵�����ɣ�
��3����չ����
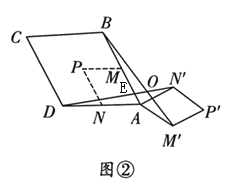
��ͼ3������1���е�Ƕ���ı���ABCD��AMPN�����dz��Ϳ�֮��Ϊ2:1�ľ��Σ���ת�ǻ�������90��������180�����������������䣬��ֱ��д��BM'��DN'��������ϵ��λ�ù�ϵ��
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ������
������![]() ��������
��������![]() ��
��![]() �ཻ���Ҽн�Ϊ
�ཻ���Ҽн�Ϊ![]() .���ɼ���������3��
.���ɼ���������3��![]() ��
��![]() .
.
��������
��1������SAS֤����ABM������AND���������õ�![]() ����ABM��=��ADN�����������������ڽǺͿ��Ƴ���BOD=90������
����ABM��=��ADN�����������������ڽǺͿ��Ƴ���BOD=90������![]() ��
��
��2��������ת�����ε�����֤��![]() �����Ƴ�
�����Ƴ�![]() ���ʿ���⣻
���ʿ���⣻
��3��������ת�;��ε�����֤��![]() ���õ�
���õ�![]() �����Ƴ�
�����Ƴ�![]() ������⣮
������⣮
��1����ͼ��![]() ��
��![]() ���ڵ�H����
���ڵ�H����
���ı���ABCD��AMPN���������Σ���������AMPN��AΪ����˳ʱ����ת150���õ�������AM'P'N'��
��AB=AD,AM��=AD��, ![]()
����ABM������AND����
��![]() ����ABM��=��ADN����
����ABM��=��ADN����
����ADN��+��DHA+��DAH=180������ABM��+��BHO+��BOD=180����
����DHA=��BHO
��![]() ����
����![]()
�ʴ�Ϊ��![]() ��
��![]() ��
��
��2��![]() ������
������![]() ��������
��������![]() ��
��![]() �ཻ���Ҽн�Ϊ
�ཻ���Ҽн�Ϊ![]() .
.
���ɣ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
����ת�����ʿɵ�![]() .
.
���ı���![]() ��
��![]() ��������
��������
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() .
.
����![]() ��
��
��![]() ��
��
��![]() ��
��![]() �ཻ���Ҽн�Ϊ
�ཻ���Ҽн�Ϊ![]() ��
��
��3��![]() ��
��![]() ���������£�
���������£�
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
����ת�����ʿɵ�![]() .
.
���ı���ABCD��AMPN�dz��Ϳ�֮��Ϊ2:1�ľ���
��![]() ��
��![]() ��
��
��![]()
��![]() ��
��
��![]() ��
��![]() .
.
����![]() ��
��
��![]()
��![]() ��
��![]() ��
��

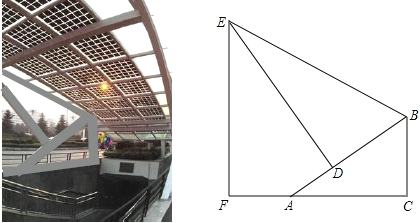
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�