题目内容
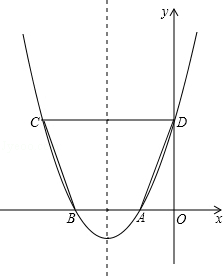
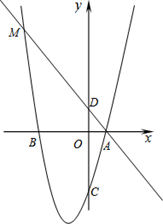
如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线 的图象过C点.
的图象过C点.
(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?
(3)点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,求出P点坐标;若不存在,说明理由.
解:(1)如答图1所示,过点C作CD⊥x轴于点D,则∠CAD+∠ACD=90°。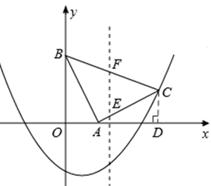
∵∠OBA+∠OAB=90°,∠OAB+∠CAD=90°,
∴∠OAB=∠ACD,∠OBA=∠CAD。
∵在△AOB与△CDA中,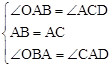 ,
,
∴△AOB≌△CDA(ASA)。
∴CD=OA=1,AD=OB=2。
∴OD=OA+AD=3。
∴C(3,1)。
∵点C(3,1)在抛物线 上,
上,
∴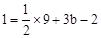 ,解得:
,解得: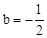 。
。
∴抛物线的解析式为: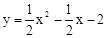 。
。
(2)在Rt△AOB中,OA=1,OB=2,由勾股定理得:AB=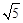 。
。
∴S△ABC= AB2=
AB2=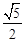 。
。
设直线BC的解析式为y=kx+b,∵B(0,2),C(3,1),
∴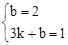 ,解得
,解得 。
。
∴直线BC的解析式为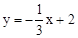 。
。
同理求得直线AC的解析式为: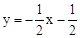 。
。
如答图1所示,设直线l与BC、AC分别交于点E、F,
则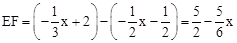 。
。
在△CEF中,CE边上的高h=OD﹣x=3﹣x.
由题意得:S△CEF= S△ABC,即:
S△ABC,即: EF•h=
EF•h= S△ABC。
S△ABC。
∴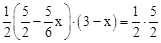 ,整理得:(3﹣x)2=3。
,整理得:(3﹣x)2=3。
解得x=3﹣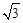 或x=3+
或x=3+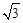 (不合题意,舍去)。
(不合题意,舍去)。
∴当直线l解析式为x=3﹣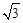 时,恰好将△ABC的面积分为相等的两部分。
时,恰好将△ABC的面积分为相等的两部分。
(3)存在。如答图2所示,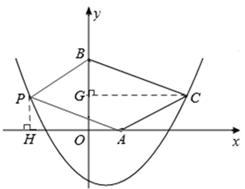
过点C作CG⊥y轴于点G,则CG=OD=3,OG=1,BG=OB﹣OG=1。
过点A作AP∥BC,且AP=BC,连接BP,则四边形PACB为平行四边形。
过点P作PH⊥x轴于点H,
则易证△PAH≌△BCG。
∴PH=BG=1,AH=CG=3,∴OH=AH﹣OA=2。
∴P(﹣2,1)。
∵抛物线解析式为: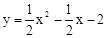 ,当x=﹣2时,y=1,即点P在抛物线上。
,当x=﹣2时,y=1,即点P在抛物线上。
∴存在符合条件的点P,点P的坐标为(﹣2,1).。
解析

已知抛物线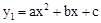 a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
| x | … | ―1 | 0 | 3 | … |
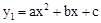 | … | 0 |  | 0 | … |
(2)若经过点T(0,t)作垂直于y轴的直线l′,A为直线l′上的动点,线段AM的垂直平分线交直线l于点B,点B关于直线AM的对称点为P,记P(x,y2).
①求y2与x之间的函数关系式;
②当x取任意实数时,若对于同一个x,有y1<y2恒成立,求t的取值范围.


 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.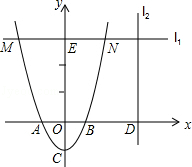
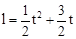 (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.