题目内容
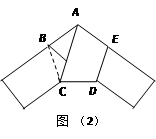
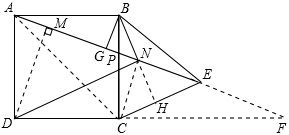
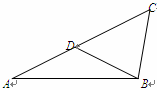
如图,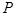 为正方形
为正方形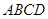 边
边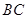 上任一点,
上任一点,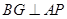 于点
于点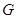 ,在
,在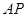 的延长线上取点
的延长线上取点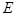 ,使
,使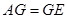 ,连接
,连接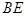 ,
,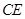 .
.
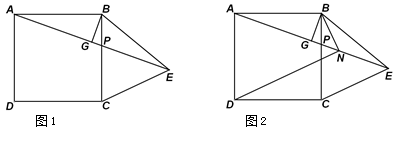
(1)求证: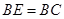 ;
;
(2)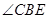 的平分线交
的平分线交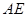 于
于 点,连接
点,连接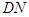 ,求证:
,求证: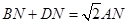 ;
;
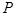 为正方形
为正方形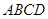 边
边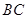 上任一点,
上任一点,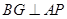 于点
于点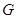 ,在
,在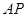 的延长线上取点
的延长线上取点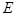 ,使
,使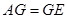 ,连接
,连接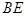 ,
,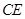 .
.
(1)求证:
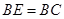 ;
;(2)
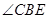 的平分线交
的平分线交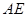 于
于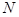 点,连接
点,连接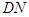 ,求证:
,求证: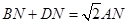 ;
;(1)由BG⊥AP,AG=GE可得BG垂直平分线段AE,根据垂直平分线的性质可得AB=BE,根据正方形的性质可得AB=BC,即可证得结论;
(2)连接CN,延长BN交CE于H,过点D作DM⊥AN于M,可证得Rt△ADM≌Rt△ABG,即得DM=AG,根据角平分线的性质可得CH=HE,即可证得△BCN≌△BEN,从而可知△CEN是等腰△,延长AE交DC延长线于F,可得∠BAG=∠BEG=∠CFE=∠BCN,则可证得Rt△DMN,Rt△BGN都是等腰直角三角形,问题得证.
(2)连接CN,延长BN交CE于H,过点D作DM⊥AN于M,可证得Rt△ADM≌Rt△ABG,即得DM=AG,根据角平分线的性质可得CH=HE,即可证得△BCN≌△BEN,从而可知△CEN是等腰△,延长AE交DC延长线于F,可得∠BAG=∠BEG=∠CFE=∠BCN,则可证得Rt△DMN,Rt△BGN都是等腰直角三角形,问题得证.
试题分析:(1)∵BG⊥AP,AG=GE,
∴BG垂直平分线段AE,
∴AB=BE,
在正方形ABCD中,AB=BC,
∴BE=BC;
(2)连接CN,延长BN交CE于H,过点D作DM⊥AN于M,
显然Rt△ADM≌Rt△ABG,
∴DM=AG,
∵BN平分∠CBE,
∴CH=HE,
∵∠CBN=∠EBN,BE=BC,BN=BN,
∴△BCN≌△BEN,
∴CN=NE,即△CEN是等腰△,
延长AE交DC延长线于F,则有∠BAG=∠BEG=∠CFE=∠BCN,
∴A,B,C,D,N五点共圆,
∴∠AND=∠BNG=45°[AB弦所对圆周角=45°]
∴Rt△DMN,Rt△BGN都是等腰直角三角形,
∴
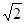 DM=
DM=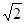 AG=DN,
AG=DN,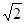 GN=BN,
GN=BN,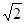 AG+
AG+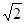 GN=
GN=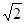 AN=BN+DN.
AN=BN+DN.点评:本题综合性较强,难度较大,准确作出辅助线,综合运用各定理和性质并分析题目用已知条件和所要证明的结论之间的关系是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

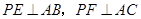 ,垂足分别为点
,垂足分别为点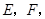
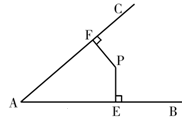
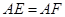 .
.
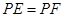 ;
;