题目内容
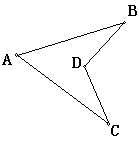
如图,在直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,点F是CD边上一点,将纸片沿BF折叠,点C落在E点,使直线BE经过点D,若BF=CF=8,则AD的长为 .


试题分析:利用等边对等角可以得到∠FBC=∠C=30°,再利用折叠的性质可以得到∠EBF=∠CBF=30°,从而可以求得∠BDF的度数,即可以求得线段BD,然后在直角三角形ABD中求解即可.
∵BF=CF=8,
∴∠FBC=∠C=30°,
∵折叠纸片使BC经过点D,点C落在点E处,BF是折痕,
∴∠EBF=∠CBF=30°,
∴∠EBC=60°,
∴∠BDF=90°
∵∠EBC=60°
∴∠ADB=60°,
∵BF=CF=8.
∴BD=BF•sin60°=

∴在Rt△BAD中,AD=BD×sin30°=
 .
.点评:解决此类题要懂得用梯形的常用辅助线,把梯形分割为矩形和直角三角形,从而由矩形和直角三角形的性质来求解.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ABC,
ABC,
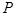 为正方形
为正方形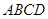 边
边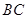 上任一点,
上任一点,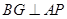 于点
于点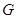 ,在
,在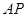 的延长线上取点
的延长线上取点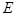 ,使
,使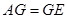 ,连接
,连接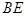 ,
,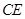 .
.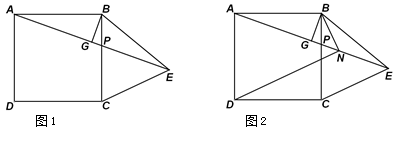
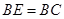 ;
;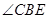 的平分线交
的平分线交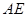 于
于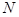 点,连接
点,连接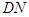 ,求证:
,求证: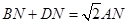 ;
;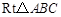 的周长为
的周长为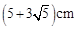 ,以
,以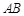 、
、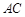 为边向外作正方形
为边向外作正方形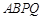 和正方形
和正方形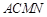 .若这两个正方形的面积之和为
.若这两个正方形的面积之和为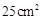 ,则
,则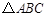 的面积是
的面积是 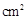 .
.