题目内容
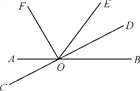
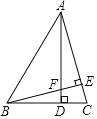
【题目】如图1,O为直线AB上一点,OC为射线,∠AOC=40°,将一个三角板的直角顶点放在点O处,一边OD在射线OA上,另一边OE与OC都在直线AB的上方.
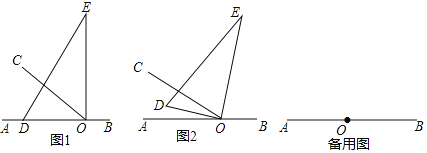
(1)将三角板绕点O顺时针旋转,若OD恰好平分∠AOC(如图2),试说明OE平分∠BOC;
(2)将三角板绕点O在直线AB上方顺时针旋转,当OD落在∠BOC内部,且∠COD=![]() ∠BOE时,求∠AOE的度数:
∠BOE时,求∠AOE的度数:
(3)将图1中的三角板和射线OC同时绕点O,分别以每秒6°和每秒2°的速度顺时针旋转一周,求第几秒时,OD恰好与OC在同一条直线上?
【答案】(1)证明见解析;(2)142.5°;(3)第10秒或第55秒时.
【解析】
(1)由角平分线的性质及同角的余角相等,可得答案;
(2)设∠COD=α,则∠BOE=3α,由题意得关于α的方程,求解即可;
(3)分两种情况考虑:当OD与OC重合时;当OD与OC的反向延长线重合时.
解:(1)∵OD恰好平分∠AOC
∴∠AOD=∠COD
∵∠DOE=90°
∴∠AOD+∠BOE=90°,∠COD+∠COE=90°
∴∠BOE=∠COE
∴OE平分∠BOC.
(2)设∠COD=α,则∠BOE=3α,当OD在∠BOC的内部时,
∠AOD=∠AOC+∠COD=40°+α
∵∠AOD+∠BOE=180°﹣90°=90°
∴40°+α+3α=90°
∴α=12.5°
∴∠AOE=180°﹣3α=142.5°
∴∠AOE的度数为142.5°.
(3)设第t秒时,OD与OC恰好在同一条直线上,则∠AOD=6t,∠AOC=2t+40°;
当OD与OC重合时,6t﹣2t=40°
∴t=10(秒);
当OD与OC的反向延长线重合时,6t﹣2t=180°+40°
∴t=55(秒)
∴第10秒或第55秒时,OD恰好与OC在同一条直线上.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】学校组织学生参加知识问答,问答活动共设有20道选择题,各题分值相同,每题必答,下表记录了A、B、C三名学生的得分情况,则参赛学生D的得分可能是( )
参赛学生 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 14 | 6 | 64 |
A.66B.93C.40D.87