题目内容
【题目】已知数轴上有A，B，C三点，分别代表﹣30，﹣10，10，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，甲的速度为4个单位/秒，乙的速度为6个单位/秒．
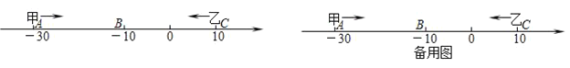
（1）甲，乙经过多少秒在数轴上相遇，并求出相遇点表示的数？
（2）多少秒后，甲到A，B，C的距离和为48个单位？
（3）在甲到A、B、C的距离和为48个单位时，若甲调头并保持速度不变，则甲，乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由．
【答案】（1）
，
；（2）3或7；（3）能，
【解析】
（1）设x秒后甲与乙相遇，根据甲与乙的路程差为40，可列出方程求解即可；
（2）设y秒后甲到A、B、C的距离和为48个单位，分甲位于AB或BC之间两种情况讨论，即可求解；
（3）设甲调头
秒后与乙在数轴上相遇，需要分类讨论：甲从A向右运动3秒时返回和甲从A向右运动7秒时返回两种情况，分别表示出甲、乙表示的数，结合线段间的和与差的关系列出方程并解答.
解：（1）设x秒后甲与乙相遇，
则
，
解得
，
，
．
故甲、乙在数轴上的点相遇；
（2）设y秒后，甲到A、B、C的距离和为48个单位，
当甲位于AB之间时：
，
解得：
；
当甲位于BC之间时：
，
解得：
；
答：3或7秒后，甲到A、B、C的距离和为48个单位；
（3）设甲调头秒后与乙相遇，
若甲从A向右运动3秒时返回，
甲表示的数为：
；乙表示的数为：
，
由题意得：
，
解得：
；
相遇点表示的数为：
.
若甲从A向右运动7秒时返回，
甲表示的数为：
；乙表示的数为：
，
由题意得：
，
解得：
；
此时甲在表示-2的点上, 乙在表示-32的点上, 乙在甲的左侧,甲追及不上乙，因而不可能相遇，故
应舍去；
答：甲从A向右运动3秒时返回，甲、乙能在数轴上相遇，相遇点表示的数为.
练习册系列答案
相关题目
