Question

【题目】如图，直线AB与CD相交于点O，OF，OD分别是∠AOE，∠BOE的平分线.

(1)写出∠DOE的补角；

(2)若∠BOE＝62°，求∠AOD和∠EOF的度数；

(3)试问射线OD与OF之间有什么特殊的位置关系？为什么？

Answer 1

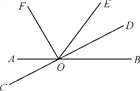
【答案】(1) ∠COE，∠AOD，∠BOC；(2)∠AOD=149°，∠EOF=59°；(3) 射线OD与OF互相垂直，理由见解析.

【解析】试题分析：（1）根据互补的定义确定∠DOE的补角；

（2）先根据角平分线的定义得出∠BOD的度数，再由邻补角定义可得∠AOD=180°-∠BOD；之后根据邻补角定义可得∠AOE=180°-∠BOE，再由角平分线的定义得出∠EOF的度数；

（3）运用平角的定义和角平分线的定义，证明∠DOF是90°，得直线OD、OF的位置关系．

解：(1)∠DOE的补角为：∠COE，∠AOD，∠BOC.

(2)∵OD是∠BOE的平分线，∠BOE＝62°，

∴∠BOD＝∠BOE＝31°.

∴∠AOD＝180°－∠BOD＝149°.

∴∠AOE＝180°－∠BOE＝118°.

又∵OF是∠AOE的平分线，

∴∠EOF＝∠AOE＝59°.

(3)射线OD与OF互相垂直.理由如下：

∵OF，OD分别是∠AOE，∠BOE的平分线，

∴∠DOF＝∠DOE＋∠EOF＝∠BOE＋∠EOA＝ (∠BOE＋∠EOA)＝×180°＝90°.

∴OD⊥OF.