题目内容
【题目】在△ABC中，AB=30，BC=28，AC=26．求△ABC的面积．
某学习小组经过合作交流给出了下面的解题思路，请你按照他们的解题思路完成解答过程．
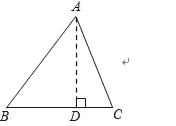
【答案】△ABC的面积为336
【解析】
根据题意利用勾股定理表示出AD2的值，进而得出等式求出答案．
解：过点D作AD⊥BC，垂足为点D．
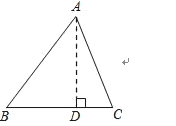
设BD=x，则CD=28﹣x．
在Rt△ABD中，AB=30，BD=x，
由勾股定理可得AD2=AB2﹣BD2=302﹣x2，
在Rt△ACD中，AC=26，CD=28﹣x，
由勾股定理可得AD2=AC2﹣CD2=262﹣（28﹣x）2，
∴302﹣x2=262﹣（28﹣x）2，
解得：x=18，
∴AD2=AB2﹣BD2=302﹣x2=302﹣182=576，
∴AD=24，
S△ABC=
BCAD=×28×24=336
则△ABC的面积为336．
练习册系列答案
相关题目
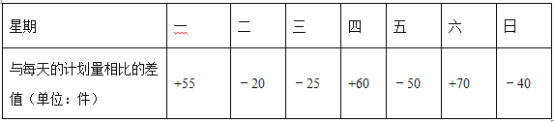
【题目】有20筐白菜，以每筐30千克为标准，超过千克数记作正数，不足的千克数记作负数，称后的记录如下表：
与标准质量的差值（单位：千克） |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 4 | 2 | 3 | 6 |
（1）20筐白菜中，最重的一筐比最轻的一筐重 千克；
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价3.5元，则出售这20筐白菜可卖多少元？
