题目内容
【题目】如图是由若干个小圆圈按一定规律拼出的一组图形：
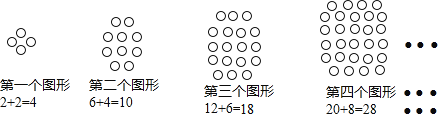
通过观察归纳可得出，第5个图形中共有_____个小圆圈，第n个图形中小圆圈的个数为_____．
【答案】40 n2+3n
【解析】
根据题目中的图形，可以写出前四个图形中小圆圈的个数，从而可以发现小圆圈个数的变化规律，从而可以求得第5个图形和第n个图形中小圆圈的个数．
解：由图可得，
第一个图形中小圆圈的个数为：1×2+1×2＝4，
第二个图形中小圆圈的个数为：2×2+2×3＝10，
第三个图形中小圆圈的个数为：3×2+3×4＝18，
第四个图形中小圆圈的个数为：4×2+4×5＝28，
…
则第5个图形中共有：5×2+5×6＝40个小圆圈，
第n个图形中小圆圈的个数为：n×2+n（n+1）＝2n+n2+n＝n2+3n，
故填：40，n2+3n．
练习册系列答案
相关题目
【题目】有20筐白菜，以每筐30千克为标准，超过千克数记作正数，不足的千克数记作负数，称后的记录如下表：
与标准质量的差值（单位：千克） |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 4 | 2 | 3 | 6 |
（1）20筐白菜中，最重的一筐比最轻的一筐重 千克；
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价3.5元，则出售这20筐白菜可卖多少元？
