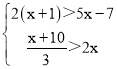题目内容
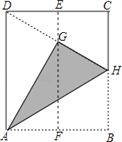
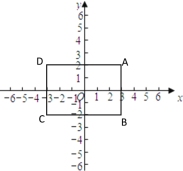
【题目】如图，在平面直角坐标系中，四边形ABCD是长方形， ∠A=∠B=∠C=∠D=90°，AB∥CD，AB=CD=4，AD=BC=6，点A的坐标为(3，2)．动点P的运动速度为每秒a个单位长度，动点Q的运动速度为每秒b个单位长度，且
.设运动时间为t，动点P、Q相遇则停止运动.
(1) 求a，b的值；
(2) 动点P，Q同时从点A出发，点P沿长方形ABCD的边界逆时针方向运动，点Q沿长方形ABCD的边界顺时针方向运动，当t为何值时P、Q两点相遇?求出相遇时P、Q所在位置的坐标；
(3) 动点P从点A出发，同时动点Q从点D出发：
①若点P、Q均沿长方形ABCD的边界顺时针方向运动，t为何值时，P、Q两点相遇?求出相遇时P、Q所在位置的坐标；
②若点P、Q均沿长方形ABCD的边界逆时针方向运动，t为何值时，P、Q两点相遇?求出相遇时P、Q所在位置的坐标.
【答案】(1)a=1,b=2；(2) 
，P、Q两点相遇，P，Q两点的坐标为
；(3)① t=6，P、Q(1,-2 )，② t=14，P、Q(1,-2 )
【解析】
（1）由
，可得
，
，从而可求出a，b的值；
（2）由相遇可得t+2t=(6+4)×2，求出t的值，进而求出相遇时P、Q所在位置的坐标；
（3）①由相遇可得方程2t-t=6 ，求出t的值，进而求出相遇时P、Q所在位置的坐标；
②由相遇可得方程2t-t=14 ，求出t的值，进而求出相遇时P、Q所在位置的坐标；
(1) ∵，
∴，，
∴a=1，b=2；
(2) ∵t+2t=(6+4)×2，
∴时，P、Q两点相遇 .
-6=
，2-=
，
∴此时P，Q两点相遇时的坐标为
；
(3) ① 2t-t=6 ， ∴t=6 ，
6-4=2，3-2=1，
∴P、Q两点相遇时的坐标为(1,-2 )；
② 2t-t=14 ， ∴t=14，
14-6-4=4，4-3=1，
∴P、Q两点相遇时的坐标为(1,-2 ).
