Question

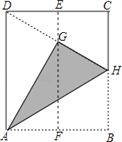
【题目】如图，在一张矩形纸片ABCD中，AD=4cm，点E，F分别是CD和AB的中点，现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH，若HG延长线恰好经过点D，则CD的长为_________．

Answer 1

【答案】

【解析】试题分析：先证明EG是△DCH的中位线，继而得出DG=HG，然后证明△ADG≌△AHG，得出∠BAH=∠HAG=∠DAG=30°，在Rt△ABH中，可求出AB，也即是CD的长．

试题解析：∵点E，F分别是CD和AB的中点，

∴EF⊥AB，

∴EF∥BC，

∴EG是△DCH的中位线，

∴DG=HG，

由折叠的性质可得：∠AGH=∠ABH=90°，

∴∠AGH=∠AGD=90°，

在△AGH和△AGD中，

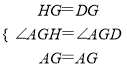
∴△ADG≌△AHG（SAS），

∴AD=AH，∠DAG=∠HAG，

由折叠的性质可得：∠BAH=∠HAG，

∴∠BAH=∠HAG=∠DAG=∠BAD=30°，

在Rt△ABH中，AH=AD=4，∠BAH=30°，

∴HB=2，AB=2，

∴CD=AB=2．