题目内容
【题目】如图,AB是⊙O的直径, BM切⊙O于点B,点P是⊙O上的一个动点(不经过A,B两点),过O作OQ∥AP交![]() 于点Q,过点P作
于点Q,过点P作![]() 于C,交
于C,交![]() 的延长线于点E,连结
的延长线于点E,连结![]() .
.
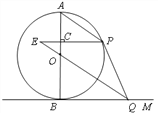
(1)求证:PQ与⊙O相切;
(2)若直径AB的长为12,PC=2EC,求tan∠E的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)连接OP,根据平行线的性质得到∠EOC=∠OAP,∠POQ=∠APO,根据等腰三角形的性质得到∠APO=∠OAP,推出△POQ≌△BOQ,根据全等三角形的性质得到∠OPQ=∠OBQ=90°,根据切线的判定定理即可得到结论;
(2)由OQ∥AP,可得△COE∽△CAP,从而列比例式![]() 求出PC的长; 由OQ∥AP,∠E=∠APC,所以tan∠E=
求出PC的长; 由OQ∥AP,∠E=∠APC,所以tan∠E=![]() ,从而求得结果.
,从而求得结果.
解:(1)连接OP,
∵OQ∥AP,∴∠A=∠BOQ,∠APO=∠POQ,
又∵OA=OP,∴∠A=∠APO.
∴∠BOQ=∠POQ,
在△OQB与△OQP中,
∠BOQ=∠POQ,OP=OB,OQ=OQ,
∴△OQB≌△OQP,
∴∠OBQ=∠OPQ,PQ=BQ.
∵BM切⊙O于点B,∴∠OBQ=∠OPQ=90°.
∴PQ与⊙O相切;
(2) ∵OQ∥AP,∴△COE∽△CAP,∴![]() ,
,
由AB的长为12,
∴OA=6.
∵PC=2EC, ∴OC=2,AC=4,
∴![]() .
.
由OQ∥AP,∠E=∠APC,
∴tan∠E=![]() .
.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】某自行车厂计划一周生产1400辆自行车,平均每天生产200辆,由于各种原因,实际每天的生产量与计划量相比有出入。
下表是某周的生产情况(超产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产了_________辆;
(2)产量最多的一天比产量最少的一天多生产__________辆;
(3)该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?