题目内容
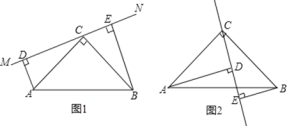
【题目】如图①,在△ABC中,∠ACB=90°,BC=AC,CE是过点C的一条直线,且A、B在CE的异侧,AD⊥CE于D,BE⊥CE于E.
(1)求证:AD=DE+BE.
(2)若直线CE绕点C旋转,使A、B在CE的同侧时(如图②),AD与DE、BE的关系如何?请予以证明.

【答案】(1)详见解析;(2)AD=DE-BE,证明详见解析.
【解析】
(1)利用垂直的定义得∠ADC=∠CEB=90°,则根据互余得∠DAC+∠ACD=90°,再根据等角的余角相等得到∠DAC=∠BCE,然后根据“AAS”可判断△ADC≌△CEB,所以CD=BE,AD=CE,再利用等量代换得到AD=DE+BE;(2)AD=DE-BE,类比(1)的方法证明△ADC≌△CEB,根据全等三角形的性质可得CD=BE,AD=CE,由此即可证得结论.
(1)证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB,
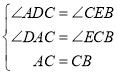 ,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴AE=CE=CD+DE=DE+BE;
(2)AD=DE-BE.
证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB,
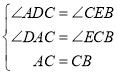 ,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴AD=EC=DE-CD=DE-BE.

练习册系列答案
相关题目