题目内容
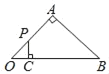
【题目】如图,在Rt△OAB中,OA=AB,∠OAB=90°,点P从点O沿边OA、AB匀速运动到点B,过点P作PC⊥OB交OB于点C,线段AB=2![]() ,OC=x,S△POC=y,则能够反映y与x之间函数关系的图象大致是( )
,OC=x,S△POC=y,则能够反映y与x之间函数关系的图象大致是( )
A. 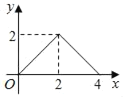 B.
B. 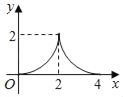
C. 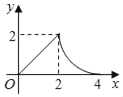 D.
D. 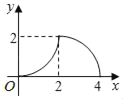
【答案】D
【解析】
分两种情况:①当P点在OA上时,即0≤x≤2时;②当P点在AB上时,即2<x≤4时,求出这两种情况下的PC长,则y=![]() PCOC的函数式可用x表示出来,对照选项即可判断.
PCOC的函数式可用x表示出来,对照选项即可判断.
解:∵△AOB是等腰直角三角形,AB=![]() ,
,
∴OB=4.
①当P点在OA上时,即0≤x≤2时,
PC=OC=x,S△POC=y=![]() PCOC=
PCOC=![]() x2,
x2,
是开口向上的抛物线,当x=2时,y=2;
②当P点在AB上时,即2<x≤4时,
OC=x,则BC=4﹣x,PC=BC=4﹣x,
S△POC=y=![]() PCOC=
PCOC=![]() x(4﹣x)=﹣
x(4﹣x)=﹣![]() x2+2x,
x2+2x,
是开口向下的抛物线,当x=4时,y=0.
综上所述,D答案符合运动过程中y与x的函数关系式.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】经过实验获得两个变量 x(x 0), y( y 0) 的一组对应值如下表。
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y | 7 | 3.5 | 2.33 | 1.75 | 1.4 | 1.17 | 1 |
(1)在网格中建立平面直角坐标系,画出相应的函数图象,求出这个函数表达式;
(2)结合函数图象解决问题:(结果保留一位小数)

①![]() 的值约为多少?
的值约为多少?
②点A坐标为(6,0),点B在函数图象上,OA=OB,则点B的横坐标约是多少?