��Ŀ����
����Ŀ�����꣬�ҹ��������������������������Υ���ж���������������������ڹ���֮�⣮��ͼ��ij���ҹ�һ�Һ��ബѲ����A�ۿ���������B��ʱ��������B�ı�ƫ��60���������150���ﴦ��C����һ���ɴ�ֻ����CA������ʻ��C����A�ۿڵı�ƫ��30�������ϣ����ബ��A�ۿڷ���ָ�ִ����������A�ۿ���AC����ʻ������D���ɹ����ؿ��ɴ�ֻ����ʱD����B��ľ���Ϊ75![]() ���
���
��1����B�㵽ֱ��CA�ľ��룻
��2��ִ������A��D�����˶��ٺ��������������ţ�

���𰸡�ִ������A��D�����ˣ�75��25![]() �����
�����
�������������������1������B��BH��CA��CA���ӳ����ڵ�H������֪�ɵá�BCA =30����
����30��������ֱ�DZߵ���б�ߵ�һ�뼴�����BH�ij�����B�㵽ֱ��CA�ľ��룻
��2����BD��BH�ij����ù��ɶ����ɵ�DH�ij�����Rt��ABH�У�����tan��BAH=![]() ���AH�ij����Ӷ��ɵ�AD�ij�.
���AH�ij����Ӷ��ɵ�AD�ij�.
�����������1������B��BH��CA��CA���ӳ����ڵ�H��
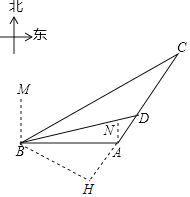
�ߡ�MBC=60�㣬
���CBA=30�㣬
�ߡ�NAD=30�㣬
���BAC=120�㣬
���BCA=180�㩁��BAC����CBA=30�㣬
��BH=BC��sin��BCA=150��![]() =75�������
=75�������
��B�㵽ֱ��CA�ľ�����75���
��2����BD=75![]() ���BH=75���
���BH=75���
��DH=![]() =75�������
=75�������
�ߡ�BAH=180�㩁��BAC=60�㣬
��Rt��ABH��tan��BAH=![]() =
=![]() ��
��
��AH=25![]() ��
��
��AD=DH��AH=��75��25![]() ���������
���������
��ִ������A��D�����ˣ�75��25![]() �����
�����