题目内容
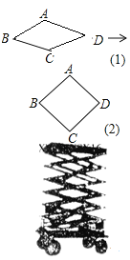
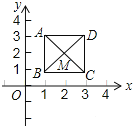
【题目】如图，已知正方形ABCD，对角线的交点M（2，2）．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（ ）
A. （﹣2012，2）B. （﹣2012，﹣2）C. （﹣2013，﹣2）D. （﹣2013，2）
【答案】A
【解析】
根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标，即可得规律：第n次变换后的点M的对应点的为：当n为奇数时为（2﹣n，﹣2），当n为偶数时为（2﹣n，2），继而求得结果．
解：∵对角线交点M的坐标为（2，2），
根据题意得：第1次变换后的点M的对应点的坐标为（2﹣1，﹣2），即（1，﹣2），
第2次变换后的点M的对应点的坐标为：（2﹣2，2），即（0，2），
第3次变换后的点M的对应点的坐标为（2﹣3，﹣2），即（﹣1，﹣2），
第n次变换后的点M的对应点的为：当n为奇数时为（2﹣n，﹣2），当n为偶数时为（2﹣n，2），
∴连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（﹣2012，2）．
故选：A．
【题目】如图，在ABCD中，AB＝3
，BC＝10，∠A＝45°，点E是边AD上一动点，将△AEB沿直线BE折叠，得到△FEB，设BF与AD交于点M，当BF与ABCD的一边垂直时，DM的长为_____．
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球（有放回），下表是活动进行中的一组统计数据．
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
（1）补全上表中的有关数据，根据上表数据估计从袋中摸出一个球是黑球的概率是 ；（精确到0.01）
（2）估算袋中白球的个数．
