Question

【题目】如图，在ABCD中，AB＝3，BC＝10，∠A＝45°，点E是边AD上一动点，将△AEB沿直线BE折叠，得到△FEB，设BF与AD交于点M，当BF与ABCD的一边垂直时，DM的长为_____．

Answer 1

【答案】4或7

【解析】

如图1，当BF⊥AD时，如图2，当BF⊥AB时，根据折叠的性质和等腰直角三角形的判定和性质即可得到结论．

解：如图1，当BF⊥AD时，

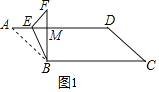
∴∠AMB＝90°，

∵将△AEB沿BE翻折，得到△FEB，

∴∠A＝∠F＝45°，

∴∠ABM＝45°，

∵AB＝3，

∴AM＝BM＝3＝3，

∵平行四边形ABCD，BC＝AD＝10，

∴DM＝AD﹣AM＝10﹣3＝7；

如图2，当BF⊥AB时，

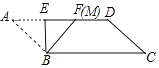
∵将△AEB沿BE翻折，得到△FEB，

∴∠A＝∠EFB＝45°，

∴∠ABF＝90°，

此时F与点M重合，

∵AB＝BF＝3，

∴AF＝3＝6，

∴DM＝10﹣6＝4．

综合以上可得DM的长为4或7．

故答案为：4或7．