Question

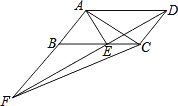
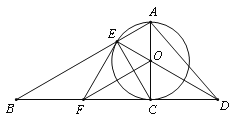
【题目】已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，作OF∥AB交BC于点F，连接EF．

（1）求证：OF⊥CE

（2）求证：EF是⊙O的切线；

（3）若O的半径为3，∠EAC＝60°，求AD的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）AD=.

【解析】试题分析: （1）根据直径所对的圆周角为直角可得CE⊥AE。根据中位线的定义可得OF为△ABC的中位线，由中位线的性质，OF//AB。根据平行线的性质，所以CE⊥OF。（2）在(1)的条件下,又有EO=OC，根据中垂线的性质，可得OF垂直平分CE，根据垂直平分线上的点到的线段两端点的距离相等，所以FC=FE，根据边边边定理可判定△OCF△OEF，根据全等三角形的性质可得OE⊥EF.根据切线性质，所以EF是⊙O的切线.

（3）根据等边三角形的判定可得△AEO为等边三角形，由等边三角形性质可得∠EOA=60°.由对顶角相等可得∠COD=∠EOA=60°.在Rt△OCD中，根据三角函数关系可得，CD=.在Rt△ACD中，根据勾股定理可得AD的长.

试题解析:

解：如图，

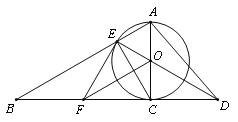
（1）证明：∵AC是⊙O的直径，

∴CE⊥AE

∵OF∥AB

∴OF⊥CE；

（2）证明：∵OF⊥CE

∴OF所在直线垂直平分CE，

∴FC＝FE

∴∠FCE＝∠FEC,

又∵OE＝OC，

∠OEC＝∠OCE,

∵∠ACB＝90°，

即∠OCE＋∠FCE＝90°，

∴∠OEC＋∠FEC＝90°，

即∠FEO＝90°，

∴FE为O的切线.

（3）∵O的半径为3，

∴AO＝CO＝EO＝3.

∵∠EAC＝60°，OA＝OE，∴△AEO为等边三角形，

∴∠EOA＝60°，

∴∠COD＝∠EOA＝60°.

∵在Rt△OCD中，∠COD＝60°，OC＝3，

∴CD＝.

∵在Rt△ACD中，∠ACD＝90°，AC＝6，

∴AD＝===.

点睛: 本题考查了切线的判定和性质，三角形的中位线的性质，勾股定理，线段垂直平分线的性质，直角三角形的性质，熟练掌握定理是解题的关键．