Question

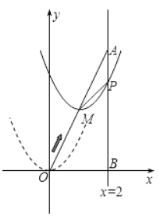
【题目】如图，BC是⊙O的直径，A是弦BD延长线上一点，切线DE平分AC于E．

（1）求证：AC是⊙O的切线；

（2）若AD∶DB=3∶2，AC=15，求⊙O的直径；

（3）在（2）的条件下，求的值；

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）连接OD，OE，求出DE＝CE，证明△ODE≌△OCE，得到∠OCE＝∠ODE＝90°即可；

（2）证明△ADC∽△ACB，得出，然后根据求出AB，由勾股定理可得答案；

（3）根据进行计算即可．

解：（1）连接OD，OE，

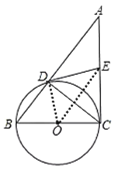
∵切线DE平分AC于E，

∴∠ODE＝90°，

∵BC是⊙O的直径，

∴∠BDC＝∠ADC＝90°，

∴在Rt△ADC中DE＝CE，

∵OE＝OE，OD＝OC，

∴△ODE≌△OCE，

∴∠OCE＝∠ODE＝90°，即OC⊥AC，

∴AC是⊙O的切线；

（2）∵∠ADC＝∠ACB＝90°，∠A＝∠A，

∴△ADC∽△ACB，

∴，

∴，

∵，

∴，

∴，，

∴；

（3）∵DE＝CE，

∴∠EDC＝∠ECD，

∴．