Question

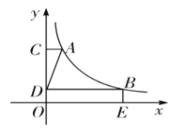
【题目】已知抛物线经过点，．把抛物线与线段围成的封闭图形记作．

（1）求此抛物线的解析式；

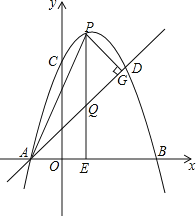
（2）点为图形中的抛物线上一点，且点的横坐标为，过点作轴，交线段于点．当为等腰直角三角形时，求的值；

（3）点是直线上一点，且点的横坐标为，以线段为边作正方形，且使正方形与图形在直线的同侧，当，两点中只有一个点在图形的内部时，请直接写出的取值范围．

Answer 1

【答案】（1）；（2）-2或-1；（3）-1≤n<1或1<n≤3.

【解析】

（1）把点，代入抛物线得关于a,b的二元一次方程组，解出这个方程组即可；

（2）根据题意画出图形，分三种情况进行讨论；

（3）作出图形，把其中一点恰好在抛物线上时算出，再确定其取值范围.

解：（1）依题意，得：

解得：

∴此抛物线的解析式 ；

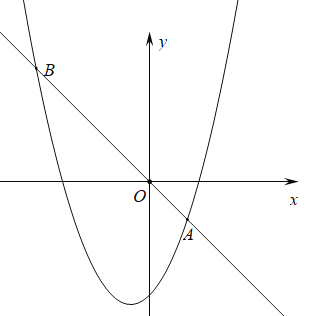
（2）设直线AB的解析式为y=kx+b,依题意得：

解得：

∴直线AB的解析式为y=-x.

∵点P的横坐标为m，且在抛物线上，

∴点P的坐标为（m, ）

∵轴，且点Q有线段AB上，

∴点Q的坐标为（m,-m）

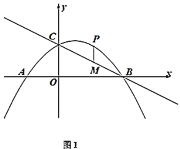
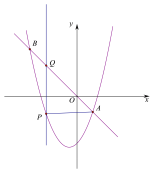
① 当PQ=AP时，如图，∵∠APQ=90°，轴，

∴

解得，m=-2或m=1（舍去）

② 当AQ=AP时，如图，过点A作AC⊥PQ于C，

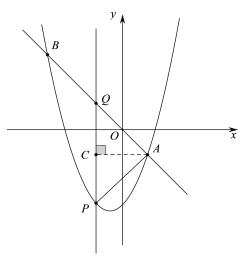
∵为等腰直角三角形，

∴2AC=PQ

即m=1(舍去)或m=-1.

综上所述，当为等腰直角三角形时，求的值是-2惑-1.；

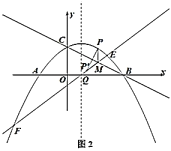
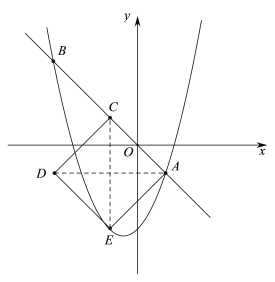
（3）①如图，当n<1时，依题意可知C,D的横坐标相同，CE=2（1-n）

∴点E的坐标为（n,n-2）

当点E恰好在抛物线上时，解得，n=-1.

∴此时n的取值范围-1≤n<1.

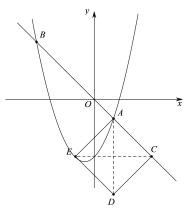
②如图，当n>1时，依题可知点E的坐标为（2-n,-n）

当点E在抛物线上时，

解得，n=3或n=1.

∵n>1.

∴n=3.

∴此时n的取值范围1<n≤3.

综上所述，n的取值范围为-1≤n<1或1<n≤3.