题目内容
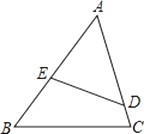
【题目】如图,等腰直角△ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( )
A.9
B.4.5
C.0
D.无法确定
【答案】B
【解析】设AC=BC=a,
∵AM=BN=3,
∴CM=a-3,CN=a+3,
∴S△AMO=S△ABC-S四边形OBCM,S△BNO=S△CMN-S四边形OBCM,
∴S△AMO-S△BNO=S△ABC-S四边形OBCM-(S△CMN-S四边形OBCM),
=S△ABC-S△CMN,
=![]() ×BC×AC-
×BC×AC-![]() ×CN×CM,
×CN×CM,
=![]() ×a×a-
×a×a-![]() ×(a+3)×(a-3),
×(a+3)×(a-3),
=![]() ×a2-
×a2-![]() ×(a2-9),
×(a2-9),
=![]() ×a2-
×a2-![]() ×a2+
×a2+![]() ,
,
=![]() .
.
所以答案是:B.
【考点精析】本题主要考查了等腰直角三角形和三角形的面积的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;三角形的面积=1/2×底×高才能正确解答此题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目