Question

【题目】已知：如图，在△ABC中，D是AC上一点，E是AB上一点，且∠AED=∠C．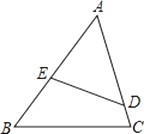
（1）求证：△AED∽△ACB；
（2）若AB=6，AD=4，AC=5，求AE的长．

Answer 1

【答案】
（1）证明：∵∠AED=∠C，∠A=∠A，

∴△AED∽△ACB.

（2）解：∵△AED∽△ACB，

∴AE：AC=AD：AB，

∵AB=6，AD=4，AC=5，

∴AE= ，

∴BE=AB-AE= .

【解析】（1）根据相似三角形的判定：两个角对应相等的两个三角形相似.
（2）由相似三角形的性质得对应边的比相等，即可求出AE的长，再由BE=AB-AE即可求出答案.
【考点精析】通过灵活运用相似三角形的判定与性质，掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．