题目内容
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③S四边形AOBO′=24+12![]() ;④S△AOC+S△AOB=24+9
;④S△AOC+S△AOB=24+9![]() ;⑤S△ABC=36+25
;⑤S△ABC=36+25![]() ; 其中正确的结论有( )
; 其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】①∵△ABC为正三角形,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,
∴∠OBO′=∠ABC=60°,OB=O′B,AB=BC,
即∠1+∠2=∠2+∠3=60°,
∴∠1=∠3,
在△BO′A和△BOC中,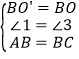 ,
,
∴△BO′A≌△BOC,
又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到;
故①正确;
②如图1:连接OO′,
∵将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,
∴∠OBO′=60°,OB=O′B,
∴△OBO′为正三角形,
又∵OB=8,
∴OO′=8;
故②正确;
③由①知△BO′A≌△BOC,
∵OC=10,
∴AO′=CO=10,
∴AO′2=AO2+OO′2,
∴△AOO′为直角三角形,
∴S四边形AOBO′=S△AOO′+S△BOO′=![]() ×6×8+
×6×8+![]() ×8×4
×8×4![]() =24+16
=24+16![]() ;
;
故③错误;
④如图2,将△AOB绕点A逆时针旋转60°,使AB与AC重合,点O旋转至O′′,
∴∠OAO′′=60°,OA=O′′A,OB=O′′C,
∵OA=6,
∴△AOO′′是边长为6的正三角形,
又∵OB=8,OC=10,
∴O′′C=8,
∴OC2=OO′′2+O′′C2,
∴△COO′′为直角三角形,
∴S△AOC+S△AOB=S△AOC+S△AO′′C=S△O′′OC+S△AO′′O=![]() ×6×8+
×6×8+![]() ×6×3
×6×3![]() =24+9
=24+9![]() ,
,
故④正确;
⑤S△AOB=![]() ×6×8×
×6×8×![]() =12,
=12,
∴S△ABC=S△AOB+S△AOC+S△BOC=S△AOB+S△ABO′+S△AOC=S△AOO′+S△BOO′+S△O′′OC+S△AO′′O-S△AOB=24+16![]() +24+9
+24+9![]() -12=36+25
-12=36+25![]() ;
;
故⑤正确;
综上所述正确的结论有:①②④⑤.
所以答案是:D.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案