题目内容
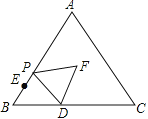
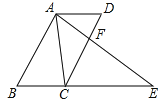
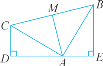
【题目】如图,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.
(1)求证:AC=BA.
(2)△ABC是什么三角形?请说明理由.
(3)如果AM⊥BC,那么AM=![]() BC吗?请说明理由.
BC吗?请说明理由.
【答案】(1)见解析;(2)△ABC是等腰直角三角形.理由见解析;(3)AM=![]() BC.理由见解析.
BC.理由见解析.
【解析】(1)AC=AB,可通过证明△ADC≌△AEB得到;
(2)△ABC是等腰直角三角形,由(1)可知△ABC是等腰三角形,再证明∠CAB=90°即可;
(3)AM=![]() BC,根据等腰三角形的性质:三线合一证明即可.
BC,根据等腰三角形的性质:三线合一证明即可.
(1)在△ACD和△BAE中,
∵CD=AE,∠CDA=∠AEB=90°,AD=BE,
∴△ACD≌△BAE(SAS).∴AC=BA.
(2)△ABC是等腰直角三角形.理由如下:
由(1)知△ACD≌△BAE,
∴AC=BA,∠CAD=∠ABE,
∴∠BAC=180°-∠CAD-∠BAE=180°-∠ABE-∠BAE=180°-90°=90°.
∴△ABC为等腰直角三角形.
(3)AM=![]() BC.理由如下:
BC.理由如下:
∵△ABC为等腰直角三角形,且AM⊥BC,
∴BM=CM,∴AM=![]() BC.
BC.

练习册系列答案
相关题目