Question

【题目】如图，在△ABC中，P为AB上一点，则下列四个条件中， ①∠ACP=∠B②∠APC=∠ACB③ ④ABCP=APCB ，
其中能满足△APC和△ACB相似的条件有（　　）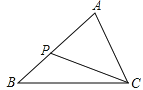

A.1个
B.2个
C.3个
D.4个

Answer 1

【答案】C
【解析】①中，∠ACP=∠B ， 又有一公共角∠A ， 所以相似，①正确； ②∠APC=∠ACB ， 且有一公共角∠A ， ②正确；
③中 AC2=APAB ， ∠A为其夹角，③正确；
④中不是两组对应边成比例，夹角相等，所以④错误．
故选：C．
【考点精析】通过灵活运用相似三角形的判定，掌握相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）即可以解答此题．