题目内容
【题目】如图,ABCD是平行四边形,点E在边BC延长线上,连AE交CD于点F , 如果∠EAC=∠D , 试问:ACBE与AECD是否相等? 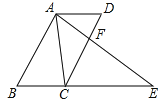
【答案】解答:∵四边形ABCD是平行四边形, ∴∠D=∠B ,
∵∠EAC=∠D ,
∴∠EAC=∠B ,
∵∠E=∠E ,
∴△ACE∽△BAE ,
∴AC:AE=AB:BE ,
即ACBE=AEAB ,
∵AB=CD ,
∴ACBE=AECD .
【解析】要证明ACBE=AECD , 只要证明这4条线段所在的三角形相似即可,但直接找不到,利用相等的线段代换后,从条件可以得出4条线段所在三角形相似从而得出结论.此题考查了相似三角形的判定和性质,利用相似三角形求出线段比,从而转化为线段的积.

练习册系列答案
相关题目