题目内容
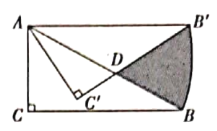
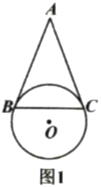
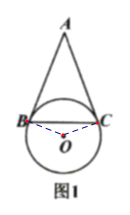
【题目】如图1,在![]() 中,
中,![]() ,以
,以![]() 为弦的
为弦的![]() 与
与![]() 相切于点
相切于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
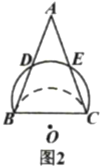
(2)将![]() 中
中![]() 以下部分沿直线
以下部分沿直线![]() 向上翻折.
向上翻折.
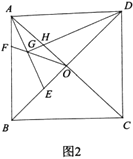
①如图2,若翻折后的弧过![]() 中点
中点![]() ,并交
,并交![]() 于点
于点![]() ,请判断
,请判断![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
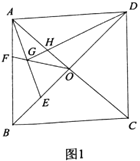
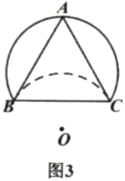
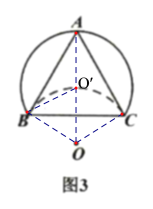
②如图3,若![]() ,且翻折后的弧恰好过点
,且翻折后的弧恰好过点![]() ,则
,则![]() 的半径为________.
的半径为________.
【答案】(1)见解析;(2)①![]() ,见解析,②2
,见解析,②2
【解析】
(1)连接OB,OC,根据等腰三角形的性质,得∠ABC=∠ACB,∠OBC=∠OCB,结合∠ABO=90°,即可得到结论;
(2)①连接DE,BE,由圆周角定理得![]() ,从而得
,从而得![]() ,进而得DE∥BC,由点D是AB的中点,可得DE是ABC的中位线,进而即可得到结论;②连接AO,BO,CO,设AO交
,进而得DE∥BC,由点D是AB的中点,可得DE是ABC的中位线,进而即可得到结论;②连接AO,BO,CO,设AO交![]() 于点O′,易得
于点O′,易得![]() 是
是![]() 所在圆的直径,记
所在圆的直径,记![]() 交弧
交弧![]() 于点
于点![]() ,两圆半径相等,那么点
,两圆半径相等,那么点![]() 就是
就是![]() 所在的圆的圆心,可得O′BO是等边三角形,再利用解直角三角形,即可得到答案.
所在的圆的圆心,可得O′BO是等边三角形,再利用解直角三角形,即可得到答案.
(1)连接OB,OC,
∵AB=AC,OB=OC,
∴∠ABC=∠ACB,∠OBC=∠OCB,
∴∠ABO=∠ACO,
∵AB是![]() 的切线,
的切线,
∴∠ABO=90°,
∴∠ACO=90°,
∴AC是![]() 的切线;
的切线;
(2)①![]() ,理由如下:
,理由如下:
连接DE,BE,
∵AB=AC,
∴∠ABC=∠ACB,
∴![]() ,
,
∴![]() ,即:
,即:![]() ,
,
∴∠BED=∠CBE,
∴DE∥BC,
∴∠ADE=∠ABC=∠ACB=∠AED,
∴AD=AE,
∵点D是AB的中点,
∴AD=![]() AB,
AB,
∴AE=![]() AC,
AC,
∴点E是AC的中点,
∴DE是ABC的中位线,
∴DE=![]() BC.
BC.
综上所述:DE∥BC,DE=![]() BC;
BC;
②连接AO,BO,CO,设AO交![]() 于点O′,
于点O′,
∵翻折后的弧恰好过点![]() ,∠ABO=90°,
,∠ABO=90°,
∴AO是![]() 所在圆的直径,
所在圆的直径,
∵![]() 所在圆与
所在圆与![]() 所在圆是等圆,
所在圆是等圆,
∴OO′既是![]() 所在圆的半径,也是
所在圆的半径,也是![]() 所在圆的半径,
所在圆的半径,
∴点O′是![]() 所在圆的圆心,
所在圆的圆心,
∴O′B=O′O=OB,
∴O′BO是等边三角形,即∠AOB=60°,
∴在RtAOB中,AO=AB÷sin60°=![]() =4,
=4,
∴OO′=2,
即:![]() 的半径为2.
的半径为2.


 天天练口算系列答案
天天练口算系列答案