题目内容
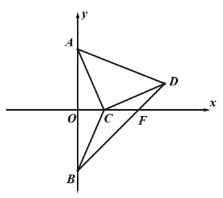
【题目】如图,正方形![]() 中.对角线AC、BD交于点
中.对角线AC、BD交于点![]() .点
.点![]() ,点
,点![]() 分别在线段
分别在线段![]() ,线段
,线段![]() 上,且
上,且![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,
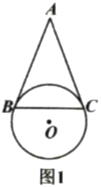
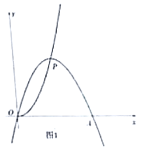
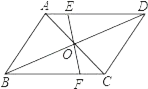
(1)如图1,若点![]() 为线段
为线段![]() 中点,
中点,![]() 求
求![]() 的长;
的长;
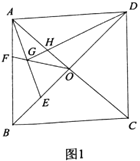
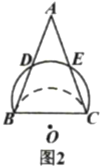
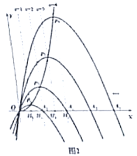
(2)如图2,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
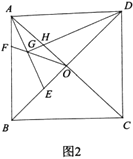
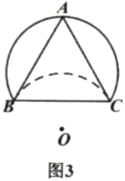
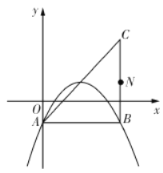
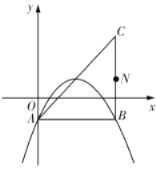
(3)如图3,点![]() 在线段
在线段![]() (含端点)上运动.连接
(含端点)上运动.连接![]() ,当线段
,当线段![]() 长度取得最大值时,直接写出
长度取得最大值时,直接写出![]() 的值.
的值.

【答案】(1)BF=![]() -1;(2)证明见解析;(3)cos∠HDO=
-1;(2)证明见解析;(3)cos∠HDO=![]() .
.
【解析】
(1)根据正方形的性质可得OA=OB,AB=![]() OB,由点E为OB的中点可得OE=
OB,由点E为OB的中点可得OE=![]() OB,利用勾股定理列方程可求出OE的长,进而可求出AB的长,根据AF=OE,即可求出BF的长;
OB,利用勾股定理列方程可求出OE的长,进而可求出AB的长,根据AF=OE,即可求出BF的长;
(2)如图,延长DG,交AB于M,根据角平分线的定义及外角的性质可得AD=DE,根据等腰三角形的性质及角的和差关系可证明DG垂直平分AE,根据直角三角形两锐角互余的性质可证明∠AMG=∠AHG,可得AM=AH,根据等腰三角形“三线合一”的性质可得MG=GH,根据∠BFO=∠AMG可得FG=MG,即可得出FG=GH;
(3)如图,连接BH,可知BH≥HE,可得当点E与点B重合时,HE取得最大值,当点E与点B重合时,OB=AF,过点F作FN⊥BD于N,设OB=x,则AB=![]() x,BF=
x,BF=![]() ,由∠ABD=45°可得△BFN是等腰直角三角形,可得BN=
,由∠ABD=45°可得△BFN是等腰直角三角形,可得BN=![]() BF,根据DN=BD-BN可表示出DN的长,利用勾股定理可得DF=
BF,根据DN=BD-BN可表示出DN的长,利用勾股定理可得DF=![]() ,根据余弦的定义即可得答案.
,根据余弦的定义即可得答案.
(1)四边形ABCD时正方形,
∴OA=OB,AB=![]() OB,
OB,
∵点![]() 为线段
为线段![]() 中点,
中点,
∴OE=![]() OB=
OB=![]() OA,
OA,
∵AE=![]() ,
,
∴OE2+(2OE)2=AE2,即5OE2=5,
解得:OE=1,(负值舍去)
∴OB=2,AB=![]() ,
,
∵AF=OE,
∴BF=AB-AF=![]() -1.
-1.
(2)如图,延长DG,交AB于M,
∵AE平分∠BAC,∠BAC=45°,
∴∠BAE=∠EAO=22.5°,
∵∠AED=∠ABE+∠BAE=45°+22.5°=67.5°,∠DAE=∠DAO+∠EAO=45°+22.5=67.5°,
∴∠AED=∠DAE,
∴AD=DE=AB,
∵OE=AF,
∴AB-AF=DE-OE,即OD=BF,
∵OD=OB,
∴OB=BF,
∴∠BOF=∠BFO=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠AOG=90°-∠BOF=22.5°,∠BOF=∠AED,
∴EG=OG,∠EAO=∠AOG,
∴AG=EG=OG,
∴DG垂直平分AE,
∴∠AMG=90°-∠BAE=67.5°,∠AHG=90°-EAO=67.5°,
∴∠AMG=∠AHG=∠BFO,
∴FG=MG,AM=AH,
∵∠BAE=∠EAO,
∴MG=GH,
∴FG=GH.
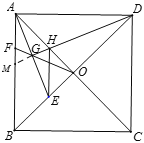
(3)如图,连接BH,
∵点E在OB上运动,∠BOH=90°,
∴BH≥HE,
∴当点E与点B重合时,HE取最大值,
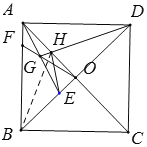
如图,当点E与点B重合时,过点F作FN⊥BD于N,设OB=x,则AB=![]() ,
,
∵OE=AF,
∴BF=(![]() -1)x,
-1)x,
∵∠ABO=45°,
∴△FBN是等腰直角三角形,
∴BN=![]() BF=
BF=![]() x,
x,
∴DN=BD-BN=2x-![]() x=
x=![]() x,
x,
∵AF=x,AD =AB =![]() x,
x,
∴DF=![]() =
=![]() x,
x,
∴cos∠HDO=![]() =
=![]() .
.
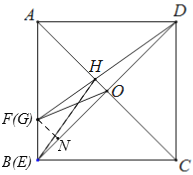

 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】2020年2月9日起,受新冠疫情影响,重庆市所有中小学实行“线上教学”,落实教育部“停课不停学”精神.某重点中学初![]() 级为了落实教学常规,特别要求家校联动,共同保证年级
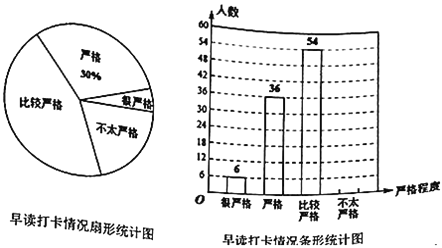
级为了落实教学常规,特别要求家校联动,共同保证年级![]() 名学生上网课期间的学习不受太大影响.为了了解家长配合情况,年级对家长在“钉钉”上早读打卡的严格程度进行了调查,调查结果分为“很严格”,“严格”,“比较严格”和“不太严格”四类.年级抽查了部分家长的调查结果,绘制成如图所示的扇形统计图和条形统计图.
名学生上网课期间的学习不受太大影响.为了了解家长配合情况,年级对家长在“钉钉”上早读打卡的严格程度进行了调查,调查结果分为“很严格”,“严格”,“比较严格”和“不太严格”四类.年级抽查了部分家长的调查结果,绘制成如图所示的扇形统计图和条形统计图.
接着,年级对早读打卡“不太严格”的全体学生进行了第一次基础知识检测,同时召开专题家长会提醒,督促这些家长落实责任,并告知将再次进行检测.两周后,年级又对之前早读打卡“不太严格”的这部分学生进行了第二次基础知识检测.
[整理、描述数据]
以下是抽查的家长打卡“不太严格”的对应学生的两次检测(满分均为![]() 分)情况:
分)情况:
分数段 |
|
|
|
|
|
第一次人数 |
|
|
|
|
|
第二次人数 |
|
|
|
|
|
[分析数据]:
众数 | 中位数 | 平均数 | |
第一次 |
|
|
|
第二次 |
|
|
|
请根据调查的信息
(1)本次参与调查的学生总人数是___,并补全条形统计图;
(2)计算![]() ____,
____,![]() ____,并请你估计全年级所有被检测学生中,第二次检测得分不低于
____,并请你估计全年级所有被检测学生中,第二次检测得分不低于![]() 分的人数;
分的人数;
(3)根据调查的相关数据,请选择适当的统计量评价学校对早读打卡“不太严格”的家长召开专题家长会的效果.