题目内容
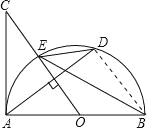
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.

【答案】(1)AC与⊙O相切,证明参见解析;(2)![]() .
.
【解析】
试题分析:(1)由于OC⊥AD,那么∠OAD+∠AOC=90°,又∠BED=∠BAD,且∠BED=∠C,于是∠OAD=∠C,从而有∠C+∠AOC=90°,再利用三角形内角和定理,可求∠OAC=90°,即AC是⊙O的切线;(2)连接BD,AB是直径,那么∠ADB=90°,在Rt△AOC中,由于AC=8,∠C=∠BED,cos∠BED=![]() ,利用三角函数值,可求OA=6,即AB=12,在Rt△ABD中,由于AB=12,∠OAD=∠BED,cos∠BED=
,利用三角函数值,可求OA=6,即AB=12,在Rt△ABD中,由于AB=12,∠OAD=∠BED,cos∠BED=![]() ,同样利用三角函数值,可求AD.
,同样利用三角函数值,可求AD.
试题解析:(1)AC与⊙O相切.∵弧BD是∠BED与∠BAD所对的弧,∴∠BAD=∠BED,∵OC⊥AD,∴∠AOC+∠BAD=90°,∴∠BED+∠AOC=90°,即∠C+∠AOC=90°,∴∠OAC=90°,∴AB⊥AC,即AC与⊙O相切;(2)连接BD.∵AB是⊙O直径,∴∠ADB=90°,在Rt△AOC中,∠CAO=90°,∵AC=8,∠ADB=90°,cos∠C=cos∠BED=![]() ,∴AO=6,∴AB=12,在Rt△ABD中,∵cos∠OAD=cos∠BED=
,∴AO=6,∴AB=12,在Rt△ABD中,∵cos∠OAD=cos∠BED=![]() ,∴AD=ABcos∠OAD=12×
,∴AD=ABcos∠OAD=12×![]() =
=![]() .
.

【题目】(6分)小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
(1)如果n=7,则S的值为 ;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.
