题目内容
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弧AE=弧BD,BE⊥DC交DC的延长线于点E.
(1)求证:∠1=∠BCE;
(2)求证:BE是⊙O的切线;
(3)若EC=1,CD=3,求cos∠DBA.

【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)过点B作BF⊥AC于点F,证△ABF≌△DBE(AAS),得BF=BE,又BE⊥DC,BF⊥AC,所以,∠1=∠BCE;(2)连接BO,证∠BAC=∠EBC,由OA=OB,得∠BAC=∠OBA,∠EBC=∠OBA,所以,∠EBC+∠CBO=∠OBA+∠CBO=90°,根据切线的判定得出即可;(3)由(2)可知:∠EBC=∠CBF=∠BAC,证△EBC≌△FBC(AAS),得CF=CE=1,由(1)可知:AF=DE=4,AC=CF+AF=5,故cos∠DBA=cos∠DCA=![]() =
=![]() .
.
(1)过点B作BF⊥AC于点F,
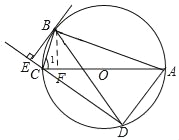
在△ABF与△DBE中,
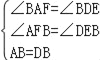
∴△ABF≌△DBE(AAS)
∴BF=BE,
∵BE⊥DC,BF⊥AC,
∴∠1=∠BCE
(2)连接OB,
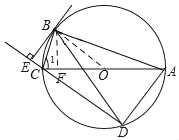
∵AC是⊙O的直径,
∴∠ABC=90°,即∠1+∠BAC=90°,
∵∠BCE+∠EBC=90°,且∠1=∠BCE,
∴∠BAC=∠EBC
∵OA=OB,
∴∠BAC=∠OBA,
∴∠EBC=∠OBA,
∴∠EBC+∠CBO=∠OBA+∠CBO=90°,
∴BE是⊙O的切线
(3)由(2)可知:∠EBC=∠CBF=∠BAC,
在△EBC与△FBC中,
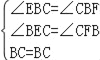
∴△EBC≌△FBC(AAS)
∴CF=CE=1
由(1)可知:AF=DE=1+3=4,
∴AC=CF+AF=1+4=5,
∴cos∠DBA=cos∠DCA=![]() =
=![]()

练习册系列答案
相关题目