题目内容
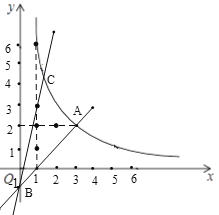
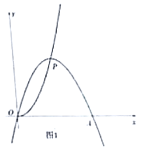
【题目】在平面直角坐标系xOy中，函数
的图象G经过点
，直线
与y轴交于点B，与图象G交于点C.
（1）求m的值.
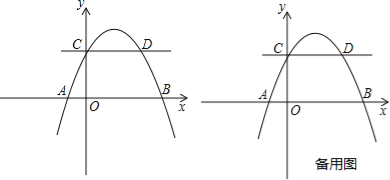
（2）横、纵坐标都是整数的点叫做整点.记图象G在点A，C之间的部分与线段BA，BC围成的区域（不含边界）为W.
①当直线l过点
时，直接写出区域W内的整点个数.
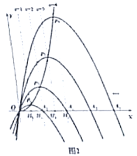
②若区域W内的整点不少于4个，结合函数图象，求k的取值范围.
【答案】（1）m=6；（2）①1个；②k>4.
【解析】
（1）把点A坐标代入
，求出m的值即可；
（2）①把点（2，0）代入y=kx-1，可求出直线l解析式，联立反比例函数解析式可求出C点坐标，画出图象，根据整点的定义即可得答案；②由直线l解析式可得B点坐标为（0，-1），利用待定系数法可得直线AB的解析式，可得B点坐标为（0，-1），当点C在点A下方时，可得整点最多有3个，不符合题意，当点C在点A上方时，根据直线AC经过整点（1，3）时有3个整点，把（1，3）代入y=kx-1，可求出k的值，整点不少于4个即可得k的取值范围.
（1）∵函数的图象G经过点
，
∴2=
，
解得：m=6.
（2）①如图，∵直线l经过（2，0），
∴2k-1=0，
解得：k=
，
∴直线l的解析式为y=x-1，
∴点（4，1）在直线l上，
∴
，
解得：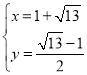
，或
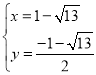（舍去），
∴点C坐标为（
，
），
∵直线l的解析式为y=kx-1，与y轴交于点B，
∴点B坐标为（0，-1），
设直线AB的解析式为y=mx+n，
∵A（3，2），B（0，-1），
∴
，
解得：
,
∴直线AB的解析式为y=x-1，
∴点（2，1）在直线AB上，
∵4<<5，1<<2，
∴区域W内的整点个数只有（3，1），共1个.
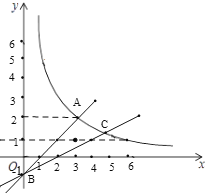
②当点C在点A下方时，
如图，当y=1时，
，
解得：x=6，
∴点C坐标为（6，1），
∵y=
(x>0)的函数值y随x的增大而减小，
∴x>6时，没有整点，
∴最多有（3，1），（4，1），（5，1）三个整点，不符合题意，
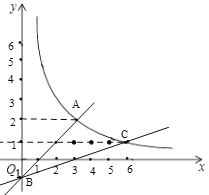
当点C在点A上方时，
如图，当x=2时，反比例函数y=
=3，一次函数y=2-1=1，
∴当x=2时有一个整点（2，2），
∵整点不少于4个，
∴x=1时，整点数应不少于3个，
∴整点为（1，1），（1，2），（1，3），
当直线AC经过（1，3）时，k-1=3，
解得：k=4，
∴k>4时，区域W内的整点不少于4个.
