题目内容
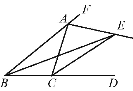
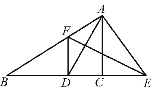
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线分别交AB于点F,交BC的延长线于点E.
求证:(1)∠EAD=∠EDA;
(2)DF∥AC.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)由AD的垂直平分线分别交AB、BC延长线于F、E,根据线段垂直平分线的性质,易得AE=DE,又由等边对等角的性质,证得∠EAD=∠EDA
(2)由AD的垂直平分线分别交AB、BC延长线于F、E,可得AF=DF,又由AD是∠BAC平分线,易得∠FDA=∠CAD,即可判定DF∥AC;
(1)∵EF是AD的垂直平分线,∴AE=DE,
∴∠EAD=∠EDA.
(2)∵EF是AD的垂直平分线,∴AF=DF,
∴∠FAD=∠FDA,
∵AD是∠BAC的平分线,∴∠FAD=∠CAD,
∴∠FDA=∠CAD,∴DF∥AC.

练习册系列答案
相关题目