题目内容
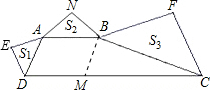
梯形ABCD中AB∥CD，∠ADC+∠BCD=90°，以AD、AB、BC为斜边向外作等腰直角三角形，其面积分别是S1、S2、S3，且S1+S3=4S2，则CD=（ ）
| A．2.5AB | B．3AB | C．3.5AB | D．4AB |
过点B作BM∥AD，
∵AB∥CD，∴四边形ADMB是平行四边形，
∴AB=DM，AD=BM，
又∵∠ADC+∠BCD=90°，
∴∠BMC+∠BCM=90°，即△MBC为Rt△，
∴MC2=MB2+BC2，
∵以AD、AB、BC为斜边向外作等腰直角三角形，
∴△AED∽△ANB，△ANB∽△BFC，
=
，
=
，
即AD2=
，BC2=
，
∴MC2=MB2+BC2=AD2+BC2=
+=
=
，
∵S1+S3=4S2，
∴MC2=4AB2，MC=2AB，
CD=DM+MC=AB+2AB=3AB．
故选B．
∵AB∥CD，∴四边形ADMB是平行四边形，
∴AB=DM，AD=BM，
又∵∠ADC+∠BCD=90°，
∴∠BMC+∠BCM=90°，即△MBC为Rt△，
∴MC2=MB2+BC2，
∵以AD、AB、BC为斜边向外作等腰直角三角形，
∴△AED∽△ANB，△ANB∽△BFC，
| S1 |
| S2 |
| AD2 |
| AB2 |
| S2 |
| S3 |
| AB2 |
| BC2 |
即AD2=
| S1AB2 |
| S2 |
| S3AB2 |
| S2 |
∴MC2=MB2+BC2=AD2+BC2=
| S1AB2 |
| S2 |
| S3AB2 |
| S2 |
| AB2(S1+S3) |
| S2 |
∵S1+S3=4S2，
∴MC2=4AB2，MC=2AB，
CD=DM+MC=AB+2AB=3AB．
故选B．
练习册系列答案
名校课堂系列答案
相关题目
